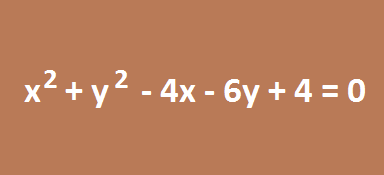Confira aqui qual é e como pode ser determinada a equação geral da circunferência no plano cartesiano.
Não deixe de ver também nossos outros tópicos sobre a geometria analítica.
Bom estudo!
A equação geral da circunferência nada mais é do que o desenvolvimento dos quadrados da equação reduzida. Veja:
(x – a)² + (y – b)² = R²
x² – 2ax + a² + y² – 2by + b² = R²
x² – 2ax + a² + y² – 2by + b² – R² = 0
x² + y² – 2ax – 2by + a² + b² – R² = 0
Exemplo 1. Determinar a equação geral da circunferência de centro C(1, 2) e raio 3.
(x – a)² + (y – b)² = R²
(x – 1)² + (y – 2)² = 3²
x² – 2x + 1 + y² – 4y + 4 = 9
x² – 2x + 1 + y² – 4y + 4 – 9 = 0
x² + y² – 2x – 4y – 4 = 0
COMPLETANDO OS QUADRADOS
Como vimos, sabendo o raio e as coordenadas da circunferência, podemos facilmente determinar a equação geral. Vamos agora fazer o processo inverso, ou seja, de posse de uma equação, vamos aprender a determinar qual é a circunferência representada, e até mesmo se essa equação representa de fato uma circunferência.
Utilizaremos um processo prático que consiste em completar os quadrados, de modo que a equação geral se torne uma equação reduzida.
Exemplo 2. Determinar a circunferência representada pela equação abaixo:
x² + y² – 4x – 6y + 4 = 0
Analisando a incógnita x
(x – a)² = x² – 2ax + a²
A equação dada possui x² – 4x.
x² – 2ax + a² = x² – 4x + ……
Nosso objetivo é descobrir qual é o valor que está faltando, ou seja, o valor de a².
Como -2ax = -4x, podemos concluir que a = 2 e que a² = 4.
Daí, o termo que está faltando é o 4.
Analisando a incógnita y
(y – b)² = y² – 2by + b²
A equação dada possui y² – 6y.
y² – 2by + b² = y² – 6y + ……
Nosso objetivo é descobrir qual é o valor que está faltando, ou seja, o valor de b².
Como -2by = -6x, podemos concluir que b = 3 e que b² = 9.
Daí, o termo que está faltando é o 9.
Voltando à equação geral da circunferência:
x² + y² – 4x – 6y + 4 = 0
x² – 4x + ……. + y² – 6y + …….. = -4
Veja que temos condições de completar os quadrados pois já descobrimos os valores que estão faltando. Temos que observar apenas que trata-se de uma igualdade, e para que isso não se altere, se somarmos um número de um lado da equação, também deveremos somá-lo do outro lado. Veja:
x² – 4x + ……. + y² – 6y + …….. = -4
x² – 4x + 4 + y² – 6y + 9 = -4 + 4 + 9
(x² – 4x + 4) + (y² – 6y + 9) = 9
(x – 2)² + (y – 3)² = 3²
Analisando a equação acima, podemos concluir que a circunferência possui centro em C(2, 3) e raio igual a 3.
ANALISANDO OS COEFICIENTES
Existem algumas condições para que uma equação da forma Ax² + By² + Cxy + Dx + Ey + F = 0 represente uma circunferência. Veja:
- A = B ≠ 0. Os coeficientes A e B devem ser iguais e diferentes de zero.
- C = 0. Não pode haver termo xy.
- D² + E² – 4AF > 0. Essa condição garante que r² > 0.
Gostou do nosso post sobre a equação geral da circunferência?
Curta e compartilhe nas redes sociais.