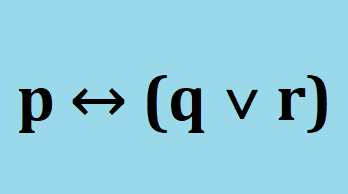Estudando raciocínio lógico para concursos? Confira aqui tudo o que você precisa saber sobre os conectivos lógicos.
Lembrando que temos outras publicações sobre o raciocínio lógico na sessão material didático.
Bom estudo!
INTRODUÇÃO
Os conectivos lógicos são utilizados para operar as proposições simples, transformando-as em proposições compostas. Eles são de suma importância para a interpretação das questões nas provas de concursos.
São eles: “e”, “ou”, “se, então”, “se, e somente se” e “ou… ou…”.
CONJUNÇÃO
A conjunção une duas ou mais proposições pelo conectivo “e”.
Símbolo utilizado: ∧
Exemplo:
p: Pedro tem uma bicicleta
q: Pedro tem um carro
p ∧ q: Pedro tem uma bicicleta e um carro.
A proposição composta resultante da conjunção será verdadeira apenas quando ambas forem verdadeiras. Veja:
DISJUNÇÃO INCLUSIVA
A disjunção inclusiva une duas ou mais proposições através do conectivo “ou”.
Símbolo utilizado: ∨
Exemplo:
p: Eu gosto de Matemática.
q: Eu gosto de Física
p ∨ q: Eu gosto de matemática ou de Física.
A proposição composta resultante da disjunção inclusiva será falsa apenas quando ambas forem falsas. Veja:
DISJUNÇÃO EXCLUSIVA
A disjunção exclusiva une duas ou mais proposições da seguinte forma:
Dizemos: “ou p, ou q”
Símbolo utilizado: ∨
Exemplo:
p: Ana vai morar na Bahia.
q: Ana vai morar em São Paulo.
p ∨ q: ou Ana vai morar na Bahia ou Ana vai morar em São Paulo.
A proposição composta resultante da disjunção exclusiva será verdadeira apenas quando apenas uma das proposições for verdadeira. Veja:
CONDICIONAL
O conectivo lógico condicional une duas proposições da seguinte forma:
Dizemos: “se p, então q”
Símbolo utilizado: →
Exemplo:
p: Pratico esportes
q: Tenho um bom preparo físico
p → q: Se pratico esportes, então tenho um bom preparo físico.
Veja que a condicional será falsa em apenas um caso:
BICONDICIONAL
O conectivo lógico bicondicional é formado por duas condicionais.
Utilizamos uma bicondicional quando temos p→q e q→p.
Dizemos: “p se e somente q”
Símbolo utilizado: ↔
Exemplo:
p: 5 + 3 = 9
q: 9 – 5 = 3
p ↔ q: 5+3=9 se e somente se 9-5=3
A bicondicional será verdadeira quando as proposições utilizadas possuírem o mesmo valor lógico. Veja:
Gostou da nossa publicação sobre os conectivos lógicos?
Deixe o seu comentário.