16. Perante a lei, quando alguém é preso, é presumidamente inocente, até que os fatos apurados atestem o contrário. Portanto, a princípio, deve aguardar em liberdade seu julgamento, a não ser que se entenda que a pessoa precisa ser presa para que sejam coletadas provas para o inquérito ou processo, a fim de se preservar a ordem pública ou econômica. Em 2005, os presos provisórios no Brasil eram 91 mil, hoje são 173 818, correspondendo a um aumento percentual de, aproximadamente,
(A) 95%.
(B) 91%.
(C) 81%.
(D) 98%.
(E) 85%.
Se o número de presos passou de 91000 para 173818, o aumento foi de:
173818 – 91000 = 82818
Calculando o aumento percentual:
82818/91000 = 0,91 ou 91%
17. Em uma população carcerária de 14 400 presos, há 1 mulher para cada 11 homens nessa situação. Do total das mulheres, 2/5e stão em regime provisório, correspondendo a
(A) 840 mulheres.
(B) 480 mulheres.
(C) 1 200 mulheres.
(D) 640 mulheres.
(E) 450 mulheres.
Se existe 1 mulher para cada 11 homens, a cada 12 presos, 1 é mulher. Daí, para saber a quantidade de mulheres, basta dividir o total de presos por 12:
14400/12 = 1200
Como 2/5 das mulheres estão no regime provisório:
1200.2/5 = 2400/5 = 480
18. Do total de internos em um presídio, 1/3 estuda. Dos que não estudam, 18% ainda são analfabetos e correspondem a 270 internos. Nesse caso, o total de internos que estudam é
(A) 1 500.
(B) 2 250.
(C) 850.
(D) 750.
(E) 920.
Chamando de x o total de presos que não estuda:
x.18% = 270
x.18/100 = 270
18x = 270.100
18x = 27000
x = 27000/18 = 1500
Como 1/3 estuda e 2/3 não estuda, claramente o número de presos que estuda é medade do número
de presos que não estuda.
Daí, o total de internos que estudam é:
1500/2 = 750
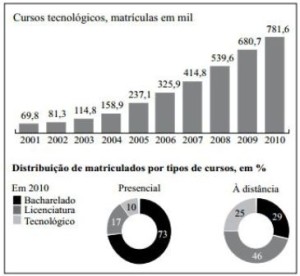
19. Observe os gráficos e analise as afirmações I, II e III.
Procura por graduação aumenta ano a ano
Explosão do número de inscritos
I. Em 2010, o aumento percentual de matrículas em cursos tecnológicos, comparado com 2001, foi maior que 1 000%.
II. Em 2010, houve 100,9 mil matrículas a mais em cursos tecnológicos que no ano anterior.
III. Em 2010, a razão entre a distribuição de matrículas no curso tecnológico presencial e à distância foi de 2 para 5.
É correto o que se afirma em
(A) I e II, apenas.
(B) II, apenas.
(C) I, apenas.
(D) II e III, apenas.
(E) I, II e III.
I. CERTO
Matrículas em 2001: 69800;
Matrículas em 2010: 781600;
Crescimento: 781600 – 69800 = 711800
Crescimento em porcentagem: 711800/69800 = 10,19 ou 119%
II. CERTO
Matrículas em 2010: 781600
Matrículas em 2009: 680700
Crescimento: 781600 – 680700 = 100900
II. CERTO
Em 2010 tivemos 10 matrículas presenciais e 25 à distância:
10/25 = 2/5
20. Os 250 trabalhadores de uma instituição serão distribuídos em frentes de trabalho, em 3 grupos de x, y e z pessoas. O número de trabalhadores x, y e z desses grupos será diretamente
proporcional a 10, 15 e 25. Nesse caso, a diferença entre a frente com maior e a frente com menor número de trabalhadores será
(A) 50.
(B) 100.
(C) 75.
(D) 45.
(E) 25.
Temos 250 trabalhadores divididos em 3 grupos, proporcionais a 10, 15 e 25.
Como 10 + 15 + 25 = 50 e 50.5 = 250, basta multiplicarmos as proporções por 5, veja:
10.5 = 50
15.5 = 75
25.5 = 125
Assim, 125 – 50 = 75
21. Para ir de casa ao trabalho, de porta a porta, Elis percorre de bicicleta 3600 metros a uma velocidade média de 300 metros por minuto. Se esse mesmo percurso fosse efetuado utilizando-se uma moto a uma velocidade média de 30 quilômetros por hora, levaria a menos que de bicicleta
(A) 4 min 48 s.
(B) 4 min 8 s.
(C) 5 min 18 s.
(D) 6 min 8 s.
(E) 7 min 2 s.
Com a bicicleta ele percorre 3600 metros a 300 metros por minuto, ele gasta:
3600/300 = 12 minutos
Com a moto sua velocidade é de 30 km por hora, como 1 hora = 60 minutos:
Sua velocidade em metros por minuto é 30000/60 = 500
Como são 3600 metros, 3600/500 = 7,2 minutos
Logo, a diferença é de 12 – 7,2 = 4,8 minutos = 4 minutos e 48 segundos
22. A média aritmética dos salários de 4 funcionários de uma empresa é R$ 2.500,00. A média aritmética dos salários dos dois primeiros é R$ 3.000,00, o quarto ganha R$ 500,00 a mais que o terceiro. Nesse caso, o salário do quarto empregado é igual a
(A) R$ 2.350,00.
(B) R$ 2.750,00.
(C) R$ 2.520,00.
(D) R$ 2.250,00.
(E) R$ 3.250,00.
Vamos chamar de x, y, z, w o salário de cada funcionários.
Como a média dos salários dos 4 é 2500:
(x + y + z + w)/4 = 2500
x + y + z + w = 4.2500
x + y + z + w = 10000 (1)
Como a média dos salários dos dois primeiros é 3000:
(x + y)/2 = 3000
x + y = 2.3000
x + y = 6000 (2)
Como o quarto ganha 500 a mais que o terceiro:
w – z = 500 (3)
Fazendo (1) – (2):
z + w = 4000 (4)
Fazendo (3) + (4):
2w = 4500
w = 4500/2 = 2250
23. Uma tenda de lona foi montada no pátio da penitenciária, com suas medidas em metros e a forma de um prisma reto indicadas na figura. A área total da lona usada na montagem foi 252 m², correspondendo à frente, ao fundo, às laterais e à cobertura.
A altura lateral (x) dessa tenda mede
(A) 3,0 m.
(B) 3,2 m.
(C) 3,5 m.
(D) 2,0 m.
(E) 4,0 m.
Área das duas laterais: 2.12x = 24x
Área do teto: 2.5.12 = 120
Área frente/atrás (4 trapézios) = 4(x+7)3/2 = 6x + 42
Daí,
24x + 120 + 6x + 42 = 252
30x = 252 – 120 – 42
30x = 90
x = 90/30 = 3
24. Um terreno ABCD está representado em uma malha quadriculada na qual o lado de cada quadradinho corresponde a 50 metros do comprimento desse terreno.
O terreno ABCD tem um perímetro de
(A) 1,8 km.
(B) 2,0 km.
(C) 3 km.
(D) 2,5 km.
(E) 1,5 km.
Para acharmos o perímetro, basta somar todos os lados.
O único que não conhecemos é o lado AD, que pode ser descoberto utilizando a fórmula de Pitágoras no triângulo retângulo:
AD² = 6² + 8²
AD² = 36 + 64
AD² = 100
AD = 10
Logo, o perímetro em quadradinhos é: 14 + 8 + 8 + 10 = 40
Como cada lado dos quadradinhos mede 50 metros, o perímetro total é 40.50 = 2000 metros
25. A quantidade de certo líquido, correspondente a 3/4 de um litro, será colocado em um recipiente de modo que ele fique completamente cheio. Para isso foram selecionados 3 recipientes com formas geométricas e medidas internas descritas a seguir:
I. Um paralelepípedo reto retângulo de dimensões: comprimento 15 cm, largura 2,5 cm e altura 20 cm.
II. Um cilindro reto de raio da base 5 cm e altura 10 cm. (use π = 3)
III. Um cubo de aresta igual a 5 cm.
Dos 3 recipientes oferecidos, atende ao que foi proposto
(A) I e II, apenas.
(B) I, II e III.
(C) I, apenas.
(D) I e III, apenas.
(E) II e III, apenas.
Temos que 1 litro pode ser colocado em um recipiente de 1000cm³
Então temos que descobrir se em algum dos 3 casos o volume é ¾ disso, ou seja, se o volume é 750cm³
I) Volume do paralelepípedo = comprimento x largura x altura = 15 x 2,5 x 20 = 750cm³
II) Volume do cilindro = área da base x altura = π.5².10 = 3.25.10 = 750cm³
III) Volume do cubo = lado³ = 5³ = 125cm³