Você já ouviu falar sobre o triângulo de Pascal? Esse triângulo, que também é conhecido como triângulo de Tartaglia, chama a atenção dos matemáticos devido as suas características especiais. Dentre as suas aplicações, podemos destacar a análise combinatória e o binômio de Newton.
Bom estudo!
O que é?
O triângulo de Pascal é uma disposição de números binominais, onde os coeficientes de mesmo numerador agrupam-se na mesma linha e os coeficientes de mesmo denominador agrupam-se em uma mesma coluna.
Veja na figura abaixo a construção de um triângulo de Pascal até a quinta linha:

Calculando o valor de cada um dos coeficientes, obtemos uma nova representação para o triângulo:
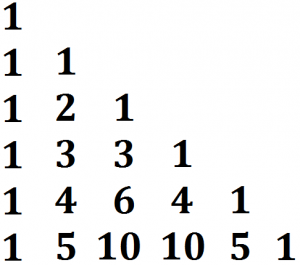
Propriedades do Triângulo de Pascal
- Todas as linhas começam e terminam por 1.
- Em uma mesma linha, os coeficientes equidistantes dos extremos são iguais. Veja na figura abaixo como os números estão dispostos na linha 5:

- Cada um dos elementos, com exceção do primeiro e do último, é igual à soma de dois elementos da linha anterior. Essa propriedade é chamada de Relação de Stifel. Veja na animação abaixo:
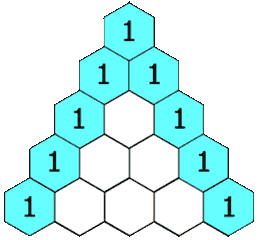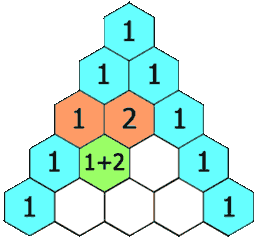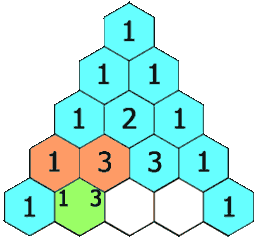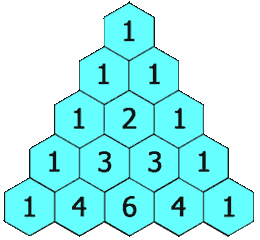
- A soma dos elementos da linha k é igual a 2k. Essa propriedade é chamada de Teorema das Linhas. Veja o exemplo da quarta linha:

- Os elementos da linha k são os coeficientes na expansão do binômio de Newton, que é um binômio da forma (a + b)k. Veja o exemplo da terceira linha:
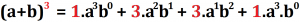
- É possível extrair a sequência de Fibonacci do triângulo de Pascal. Observe as diagonais marcadas pelas linhas vermelhas, cujas somas formam a sequência.

- As potências de 11 podem ser obtidas a partir das linhas do triângulo, onde a potência 11k está localizada na linha k. É importante ressaltar que a partir da quinta linha já aparecem números com mais de um algarismo. Neste caso, os algarismos que não correspondem à unidade podem ser acrescentados à próxima potência de 10. Veja o exemplo da linha 4:
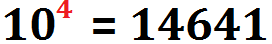
Aprendeu a identificar um Triângulo de Pascal?
Deixe o seu comentário.
