Estudando matemática para concursos? Confira aqui como podemos resolver questões através da regra de três composta.
Trata-se de uma ferramenta muito útil e utilizada para resolver problemas de razão e proporção com várias variáveis.
Bom estudo!
A regra de três composta é uma ferramenta da matemática utilizada na resolução de problemas com três ou mais grandezas proporcionais.
Exemplo
Em uma fábrica de tijolos existem 3 máquinas que funcionam ininterruptamente, 10 horas por dia, durante 4 dias, e produzem 120.000 tijolos. Sabendo que uma delas ficou parada por 6 dias, e que nesse período a fábrica tinha uma encomenda de 240.000 tijolos, quantas horas diárias de trabalho foram necessárias para que a encomenda fosse entregue?
O primeiro passo é observar que existem quatro grandezas:
- máquinas
- horas
- dias
- tijolos
O segundo passo é montar a tabela abaixo com as duas situações, e considerando que a incógnita x representa o valor desconhecido.

O terceiro, e mais importante, passo para resolver uma questão de regra de três composta é comparar todas as grandezas com a que possui o x, ou seja, comparar com a grandeza horas, que será considerada a nossa grandeza principal.
A dica é apontar a seta da grandeza x para cima e comparar com as demais. Caso seja diretamente proporcional, apontar a outra seta também para cima, e caso seja inversamente proporcional, apontar a outra seta para baixo.
Veja que:
- Quanto mais máquinas trabalhando, menos horas serão necessárias para concluir um serviço (inversamente proporcionais, seta para baixo).
- Quanto mais dias de trabalho, menos horas serão necessárias (inversamente proporcionais, seta para baixo).
- Quanto mais tijolos a serem fabricados, mais horas de trabalho serão necessárias (diretamente proporcionais, seta para cima).

O quarto passo será montar a equação, que será formada da seguinte forma:
- Os valores abaixo da grandeza principal (a que contém x), devem ficar do lado esquerdo da igualdade, em forma de fração.
- Todas os demais valores devem ficar do lado direito da igualdade, também em forma de fração, que devem ser multiplicadas umas pelas outras.
- As frações referente às grandezas com seta para baixo devem ser invertidas.
Resolvendo a equação:
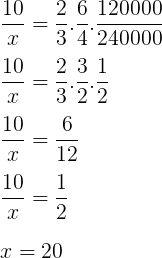
De onde concluímos que as máquinas devem trabalhar 20 horas por dia para que o prazo seja cumprido.
Gostou do nosso conteúdo sobre a regra de três composta?
Curta e compartilhe nas redes sociais.
