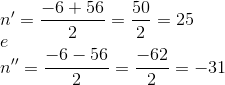Estudando para concursos? Confira a prova resolvida do concurso para a Polícia Militar do Estado do Espírito Santo realizado pela Exatus em 2013.
Comece já a estudar pelo Saber Matemática e saia na frente.
Boa sorte!
Questão 41) O comandante de um destacamento militar ordenou que seus subordinados se organizassem em filas. A primeira fila era composta por 14 soldados, a segunda por 18 soldados, a terceira por 22 soldados, e assim sucessivamente. Sabe-se que o número de soldados deste destacamento é igual a 1550. Dessa forma, é correto afirmar que serão formadas:
a) 18 filas
b) 20 filas
c) 23 filas
d) 25 filas
e) 30 filas
Resolução:
Temos uma PA, onde:
a1 = 14
r = 4
Sn = 1550
Precisamos descobrir o valor de n (número de termos)
Pela fórmula do termo geral:
an = a1 + (n – 1)r
an = 14 + (n – 1)4
an = 14 + 4n – 4
an = 4n + 10
Pela fórmula da soma dos termos:
Sn = (a1 + an)n/2
1550 = (14 + an)n/2
Vamos substituir an = 4n + 10 na segunda expressão:
1550 = (14 + 4n + 10)n/2
2.1550 = (4n + 24)n
3100 = 4n² + 24n
4n² + 24n – 3100 = 0
n² + 6n – 775 = 0
Δ = b² – 4ac
Δ = 6² – 4.1.(-775)
Δ = 36 + 3100
Δ = 3136
Assim,
Como n representa o número de filas, vamos considerar apenas o valor positivo.
Resposta: D
Questão 42) Quatro amigo, Abel, Bruno, Caio e Daniel, são colecionadores de figurinhas. Sabe-se que Abel possui metade da quantidade de figurinhas de Daniel mais um terço da quantidade de figurinhas de Caio; que Bruno possui o dobro da quantidade de figurinhas de Caio mais a quarta parte da quantidade de figurinhas de Daniel; que Daniel tem 60 figurinhas, e que Abel e Bruno possuem a mesma quantidade de figurinhas. Os quatro amigos possuem, juntos:
a) 125 figurinhas
b) 128 figurinhas
c) 130 figurinhas
d) 132 figurinhas
e) 135 figurinhas
Resolução
Tomando:
A = Abel
B = Bruno
C = Caio
D = Daniel
Pelo enunciado, temos:
A = D/2 + C/3
B = 2C + D/4
D = 60
B = A
A = D/2 + C/3
A = 60/2 + C/3
A = 30 + C/3
B = 2C + D/4
B = 2C + 60/4
B = 2C + 15
De B = A:
2C + 15 = 30 + C/3
2C – C/3 = 30 – 15
(6C – C)/3 = 15
5C/3 = 15
C = 3.15/5
C = 9
A = 30 + C/3
A = 30 + 9/3
A = 30 + 3
A = 33
B = 2C + 15
B = 2.9 + 15
B = 18 + 15
B = 33
A + B + C + D = 33 + 33 + 9 + 60 = 135
Resposta: E
Questão 43) Em determinada empresa, a cada 75 minutos de trabalho os funcionários fazem uma pausa de 15 minutos para descanso. Um funcionário em sua jornada de trabalho fez 4 pausas e encerrou seu turno de trabalho às 17h30min. Considerando que não há pausa para descanso após a última sessão de 75 minutos de trabalho, é correto afirmar que esse funcionário iniciou seu turno de trabalho às:
a) 10h
b) 10h15min
c) 10h20min
d) 10h30min
e) 10h45min
Resolução
Como ele faz 4 pausas, ele trabalhou 4 x (75 + 15) e mais ainda os últimos 75 minutos que não tem pausa:
= 4(75 + 15) + 75
= 4.90 + 75
= 360 + 75
= 435 minutos
Como cada hora tem 60 minutos, dividimos 435/60 = 7,25 horas, que corresponde a 7h15min.
Se ele encerrou às 17h30min, ele só pode ter iniciado às 17h30min – 7h15min = 10h15min.
Resposta: B
Questão 44) Lucas possui um veículo que consome um litro de combustível a cada 11 km. Ao iniciar uma viagem, abasteceu o veículo completando o tanque de combustível e, após a parada para o almoço, verificou que havia consumido 40% do combustível. Para chegar ao seu destino, foi consumido mais 35% do combustível que havia quando ele iniciou a viagem, e ainda restaram 15 litros de combustível. A distância percorrida por Lucas nessa viagem foi de :
a) 525 km
b) 505 km
c) 495 km
d) 480 km
e) 475 km
Resolução
Como ele gastou 40% + 35% e restaram 15 litros, a quantidade restante corresponde a 25% do tanque, ou seja, o tanque tem capacidade para 60 litros.
Temos então que ele gastou 75% de 60 litros = 45 litros.
Se o veículo consome 1 litro a cada 11 km, ele percorreu 45 x 11 = 495 km.
Resposta: C
Questão 45) Um estoquista, ao conferir a quantidade de determinado produto embalado em caixas cúbicas de arestas medindo 40 cm, verificou que o estoque do produto estava empilhado de acordo com a figura que segue:
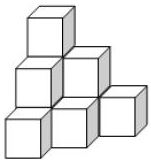Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:
a) 0,64 m³
b) 1,6 m³
c) 6,4 m³
d) 16 m³
e) 64 m³
Resolução
Temos 10 caixas cúbicas de 40 cm de aresta.
Sabe-se que 40cm = 0,4m
Cada caixa possui volume de 0,4×0,4×0,4 = 0,064m³
Como temos 10 caixas: 10 x 0,064 = 0,64m³
Resposta: E
Questão 46) Dados um cilindro circular reto e um cone circular reto de mesma altura e mesmo raio, é correto afirmar que o volume do cone é igual a:
a) três vezes o volume do cilindro
b) duas vezes o volume do cilindro
c) metade do volume do cilindro
d) terça parte do volume do cilindro
e) sexta parte do volume do cilindro
Resolução
Fórmula para cálculo de volume de cilindros
V = π.r².h
Fórmula para cálculo de volume de cones
V = (π.r².h)/3
Como altura e raio são iguais, claramente o volume do cone é 1/3 do volume do cilindro.
Resposta: D
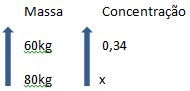
Questão 47) No Brasil, o indivíduo que dirigir alcoolizado está sujeito às normas da lei 11.705 do código de trânsito brasileiro, a “lei seca”. Tal lei estabelece, entre outras, a pena de detenção para o motorista que conduzir veículo sob efeito do álcool (etanol) a uma concentração superior a 0,34 mg de álcool por litro de ar expelido pelos pulmões (descontado o erro máximo admissível de 0,04 mg/L).
Considere que a concentração de álcool está relacionada de forma diretamente proporcional à massa corporal do indivíduo e que, para um homem de 60 kg por exemplo, ingerir 0,34 mg de álcool equivale a tomar 700 ml de determinado tipo de cerveja. Caso a massa corporal desse homem fosse de 80 kg, a concentração de álcool por litro de ar seria de:
a) 0,25 mg/L
b) 0,255 mg/L
c) 0,275 mg/L
d) 0,28 mg/L
e) aproximadamente 0,45 mg/L
Resolução
Se considerarmos verdadeira a afirmação de que massa corporal e concentração de álcool são grandezas diretamente proporcionais:
60x = 80.0,34
6x = 8.0,34
6x = 2,72
x = 2,72/6
x = 0,4533…
A resposta oficial é a letra B, que ao meu entender deveria ser realmente a correta, porém a questão afirma equivocadamente que as duas grandezas são diretamente proporcionais.
A questão deve ser anulada.
Vamos tomar dois exemplos extremos, uma pessoa muito grande e outra muito pequena, ambas tomando a mesma quantidade de cerveja. É fácil de perceber que a concentração de álcool no corpo da pessoa pequena será muito maior do que a concentração de álcool no corpo da pessoa grande, ou seja, massa corporal e concentração de álcool são grandezas inversamente proporcionais.
Questão 48) Numa urna, o número de bolas verdes é igual ao dobro do número de bolas pretas, o número de bolas roxas é igual à metade do número de bolas rosas, o número de bolas laranjas é igual ao triplo do número de bolas pretas e 65 bolas não são rosas. Se não existem bolas de outras cores e apenas 5 bolas são roxas, então o número de bolas nessa urna é igual a:
a) 68
b) 70
c) 72
d) 74
e) 75
Resolução
Sabendo que tem 5 bolas roxas, podemos concluir que tem 10 bolas rosas.
Se 65 bolas não são rosas, o total de bolas é 10 + 65 = 75
Resposta: E
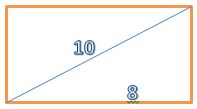
Questão 49) A diagonal de um retângulo mede 10 cm, e um de seus lados mede 8 cm. A superfície desse retângulo mede:
a) 40 cm²
b) 48 cm²
c) 60 cm²
d) 70 cm²
e) 80 cm²
Resolução
Para calcular a área precisamos saber a medida do outro lado, que pode ser descoberto pelo teorema de pitágoras:
10² = 8² + x²
100 = 64 + x²
100 – 64 = x²
36 = x²
x = 6
Área = 8.6 = 48 cm²
Resposta: B
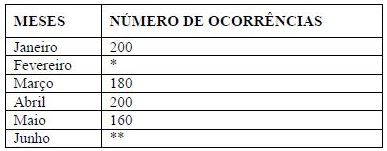
Questão 50) Determinado distrito policial registrou, em média, no primeiro semestre deste ano, 170 boletins de ocorrências por mês, conforme o quadro abaixo:
Sabe-se que em fevereiro foram registradas 20 ocorrências a menos que em junho. Portanto, o número de ocorrências registradas em junho é igual a:
a) 150
b) 145
c) 140
d) 135
e) 130
Resolução
Vamos chamar de x o número de ocorrências em junho. Logo, em fevereiro tivemos x – 20 ocorrências.
Sabendo que a média foi de 170:
(200 + x – 20 + 180 + 200 + 160 + x)/6 = 170
2x + 720 = 6.170
2x = 1020 – 720
2x = 300
x = 300/2
x = 150
Resposta: A
Questão 51) Uma equipe composta por 12 operários, trabalhando 10 horas por dia, realiza determinada obra em 45 dias. Considerando-se o mesmo ritmo de trabalho, se essa equipe fosse constituída por 15 operários, e a carga horária de trabalho fosse de 8 horas por dia, a mesma obra seria realizada em:
a) até 42 dias
b) 43 dias
c) 44 dias
d) 45 dias
e) mais de 45 dias
Resolução
Temos três grandezas:
Resposta: D
Questão 52) Laura cultiva flores em um canteiro com formato de semicírculo, cujo diâmetro mede 16 m. A área ocupada por esse canteiro é igual a:
a) 256π cm²
b) 128π cm²
c) 64π cm²
d) 32π cm²
e) 16π cm²
Resolução:
Temos que o raio mede 8 m.
Área da circunferência = π.r² = π.8² = 64π m²
A área do semicírculo será a metade: 32π m²
Claramente houve um erro de digitação e a questão é passível de anulação.
Questão 53) Assinale a alternativa correta:
a) O gráfico da função y = x² + 2x não intercepta o eixo y.
FALSA: Uma parábola sempre intercepta o eixo y.
b) O gráfico da função y = x² + 3x + 5 possui concavidade para baixo.
FALSA: O valor de a = 1 >0. Concavidade para cima.
c) O gráfico da função y = 5x – 7 é decrescente.
FALSA: O valor de a = 5 > 0. Crescente.
d) A equação x² + 25 = 0 possui duas raízes reais e diferentes.
FALSA: Nenhum número Real elevado ao quadrado fica negativo.
e) A soma das raízes da função y = x² – 3x – 10 é igual a 3.
Lembrando da fórmula da soma das raízes;
Soma = -b/a = -(-3)/1 = 3
Resposta: E
Questão 54) Para realizar o teste físico em determinado concurso da PM, os candidatos devem correr ao redor de uma praça circular cujo diâmetro mede 120 m. Uma pessoa que dá 9 voltas ao redor dessa praça percorre: (Dado: π = 3).
a) 1620 m
b) 3240 m
c) 4860 m
d) 6480 m
e) 8100 m
Resolução
Comprimento de uma circunferência = 2π.r = 2.3.60 = 360m
Como a pessoa dá 9 voltas: 9×360 = 3240m
Resposta: B
Questão 55) Altair nasceu quando Tales tinha 7 anos. Hoje, o produto de suas idades é igual a 98. Tales tem:
a) 21 anos
b) 14 anos
c) 12 anos
d) 8 anos
e) 7 anos
Resolução
T = idade de Tales
A = idade de Altair
A = T – 7
T.A = 98
T(T – 7) = 98
T² – 7T – 98 = 0
Essa é fácil resolver pelo método de soma e produto.
As raízes são dois números cuja soma é 7 e o produto é -98.
São eles -7 e 14.
Como T é a idade de Tales, vamos considerar apenas o positivo.
Resposta: B
Questão 56) Determinada cultura de bactérias, quando submetida à experiência em laboratório, triplica sua população a cada 5 minutos. Considerando uma população inicial de 4 bactérias, ao fim de uma experiência com duração de 3/4 de hora haverá:
a) 236196 bactérias
b) 157464 bactérias
c) 78732 bactérias
d) 26244 bactérias
e) 8748 bactérias
Resolução
3/4 de hora corresponde a 45 minutos, ou seja, a população é triplicada 9 vezes:
4.3.3.3.3.3.3.3.3.3 = 78732 bactérias
Resposta: C
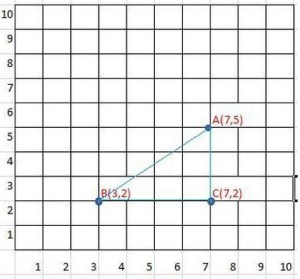
Questão 57) Clarence desenhou o triângulo determinado pelas coordenadas dos pontos cartesianos A(7;5), B(3;2) e C(7;2). Ao calcular a área e o perímetro desse triângulo, os valores obtidos foram, respectivamente:
a) 3 e 3
b) 3 e 6
c) 6 e 6
d) 6 e 12
e) 12 e 12
Resolução
Desenhando o triângulo:
Pela figura, temos um triângulo retângulo com BC = 4 e AC = 3. Vamos descobrir AB usanto teorema de pitágoras:
AB² = 4² + 3²
AB² = 16 + 9
AB² = 25
AB = 5
Perímetro = 3 + 4 + 5 = 12
Área = 3×4/2 = 6
Resposta: D
Questão 58) Em linguagem matemática, sempre que relacionamentos duas grandezas variáveis estamos empregando o conceito de função. A função y = -x + 5 é chamada função polinomial do 1º grau, e sua representação gráfica é semelhante a:
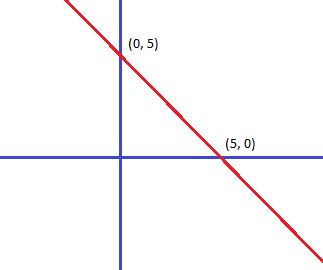
Basta sabermos que o gráfico de uma função do primeiro grau é uma reta e que o valor de “a” indica se é crescente ou decrescente, neste caso a é menor que zero, então a função é decrescente, e também que o valor de “b” indica onde a reta corta o eixo y, no caso b = 5.
Questão 59) Determinado produto custava, em maio R$ 40,00. No mês de junho sofreu aumento de 15% no seu preço de venda, e no mês de julho sofreu novo aumento de 18%. Em comparação com o mês de maio, o preço de venda desse produto em julho sofreu aumento de:
a) 33%
b) 35,7%
c) 37,5%
d) 53,7%
e) 57,3%
Resolução
Perceba que o valor do produto é irrelevante pois a questão quer apenas o aumento percentual.
Imagine que o produto custava 1 real, quando multiplicamos por 1,15, aumenta em 15%. Da mesma forma, quando multiplicamos por 1,18, aumentamos em 18%.
O produto 1 x 1,15 x 1,18 = 1,357 = 35,7%
Resposta: B
Questão 60) Uma caixa em formato de paralelepípedo reto retângulo possui largura igual ao dobro da medida da altura, e comprimento igual ao dobro do comprimento da largura. Sabe-se que o volume dessa caixa é igual a 216 cm3. A largura dessa caixa mede:
a) 2 cm
b) 3 cm
c) 6 cm
d) 12 cm
e) 18 cm
Resolução
Sejam:
L = largura
A = altura
C = comprimento
L = 2A logo A = L/2
C = 2L
Volume = largura x altura x comprimento = 216
L x A x C = 216
L x L/2 x 2L = 216
L x L x L = 216
L³ = 216
L = 6
Resposta: C
Questão 61) O quarto termo de uma progressão aritmética vale 18. A soma dos sete primeiros termos dessa PA é igual a:
a) 126
b) 120
c) 110
d) 56
e) 30
Questão incompleta.
Basta observar que a única informação é que o quarto termo vale 18. Ora, podemos imaginar infinitas PA’s com essa característica.
Questão 62) José Carlos escreveu as seguintes simbologias em seu caderno:
A : 12 = 3
B X B = A
B X A = C
C : D = 3A
Em seguida, ele desafiou Alberto a realizar a soma “A – B + C – D”, coisa que Alberto fez corretamente, obtendo resultado igual a:
a) 189
b) 206
c) 224
d) 244
e) 260
Resolução
A = 3.12 = 36
B² = 36, logo B = 6
C = BxA = 6 X 36 = 216
D = C/3A = 216/3 X 36 = 2
A – B + C – D = 36 – 6 + 216 – 2 = 244
Resposta: D
63) Anderson, Brunoro e Caio montaram uma empresa de informática. Para abrir a empresa, os três investiram, juntos, 80 mil reais. Anderson investiu 30 mil reais, Brunoro 70% do valor do investimento de Anderson, e Caio investiu o restante. Após o primeiro ano de operações, a empresa apresentou lucro de 25 mil reais, dos quais, 4/5 seriam retirados pelos sócios. A parte que coube a Caio foi de:
a) R$ 5250,00
b) R$ 6250,00
c) R$ 7250,00
d) R$ 7500,00
e) R$ 7750,00
Resolução
Anderson = 30 mil
Brunoro = 70% de 30 mil = 21 mil
Caio = 29 mil pois o total é 80 mil.
4/5 de 25 mil = 20 mil
Cabe a caio 29/80 de 20000 = 580000/80 = 7250
Resposta: C
Questão 64) Determinada obra foi iniciada por um grupo de 15 operários, que deveriam realizá-la, segundo a previsão da empresa responsável, em 145 dias de trabalho. Após o sexagésimo quinto dia, foram contratados mais 5 operários para trabalharem na obra. Respeitando-se o ritmo de trabalho previsto para cada trabalhador, é correto afirmar que essa obra foi realizada em:
a) 172 dias
b) 125 dias
c) 107 dias
d) 79 dias
e) 60 dias
Resolução
15 operários trabalharam 65 dias
Note que os 15 gastariam 80 dias.
Vamos utilizar regra de três:
Quanto mais operários, menos dias. Grandezas inversamente proporcionais:
20x = 15.80
20x = 1200
x = 1200/20 = 60 dias
Total: 65 + 60 = 125 dias
Resposta: B
Questão 65) Em determinada localidade, sabe-se que há 14.000 homens, e que 3/5 dos habitantes são mulheres. O número total de habitantes dessa localidade é igual:
a) 18000
b) 21000
c)25000
d) 28000
e) 35000
Resolução
Como 3/5 são mulheres, então 2/5 são homens.
Tomando x = população total.
x.2/5 = 14000
x = 14000.5/2
x = 70000/2
x = 35000
Resposta: E
Questão 66) Determinado cubo possui volume de 729 cm³. Cada face desse cubo possui área de:
a) 3 cm²
b) 9 cm²
c) 27 cm²
d) 54 cm²
e) 81 cm²
Resolução
O volume do cubo é 729 cm³
Fórmula do volume é:
V = x³, onde x é o lado do cubo
729 = x³
x = 9 cm
Calculando a área:
A = x² = 9² = 81 cm²
Resposta: E
Questão 67) Eduardo tinha, há 2 anos atrás, a triplo da idade de sua irmã Cláudia. Hoje, o produto de suas idades é igual a 84. A diferença de idade entre Eduardo e Cláudia é de:
a) 8 anos
b) 7 anos
c) 6 anos
d) 5 anos
e) 4 anos
Resolução
Tomando:
E = idade de Eduardo
C = idade de Cláudia
Temos:
“Eduardo tinha, há 2 anos atrás, o triplo da idade de sua irmã Cláudia.” é equivalente a:
E – 2 = 3(C – 2)
E- 2 = 3C – 6
E = 3C – 6 + 2
E = 3C – 4
“Hoje, o produto de suas idades é igual a 84” é equivalente a:
E.C = 84
Substituindo a primeira na segunda equação:
C(3C – 4) = 84
3C² – 4C – 84 = 0
Δ = b² – 4ac = (-4)² – 4.3.(-84) = 16 + 1008 = 1024
C = (-b +- √Δ) / 2a
C = (-(-4) +- √1024) / 2.3
C = (4) +- 32) / 6
Como C é a idade de Cláudia, tomaremos apenas o valor positivo.
C = (4 + 32) / 6 = 36 / 6 = 6
Vamos calcular o valor de E:
E = 3C – 4 = 3.6 – 4 = 18 – 4 = 14
Fazendo a diferença:
E – C = 14 – 6 = 8
Resposta: A
Questão 68) Sabe-se que a população de determinada cidade é de 5.000.000 habitantes, e que 35% dessa população tomou a vacina contra gripe, sendo que 60% das pessoas vacinadas eram crianças. Portanto, o número de crianças que tomaram a vacina contra gripe é igual a;
a) 1,05 x 104
b) 1,05 x 105
c) 1,05 x 106
d) 1,75 x 105
e) 1,75 x 106
Resolução:
5000000.35/100 = 175000000/100 = 1750000
1750000.60/100 = 1050000 = 1,05×106
Resposta: C
69) Aldo aplicou um capital de R$ 975,00 à taxa de juros simples de 37,5% a.a., com a intenção de fazer a retirada do montante quando o valor referente aos juros dessa aplicação fosse equivalente ao dobro do capital aplicado. Portanto, o prazo de aplicação desse capital é de;
a) 8 anos
b) 5,5 anos
c) 5 anos e 5 meses
d) 5 anos e 4 meses
e) 5 anos e 3 meses
Resolução
Para que os juros cheguem ao dobro do capital, este deve chegar a 200%
Tomando x = prazo
37,5x = 200
x = 200/37,5
x = 5,333…
x = 5 anos e 4 meses
Resposta: D
Questão 70) Um veículo com motor flex pode ser abastecido com álcool e/ou gasolina. Caso seja abastecido com 30 litros de gasolina, ao preço de R$ 2,90 o litro, e 20 litros de álcool, a R$ 1,80 o litro, o preço médio do litro de combustível utilizado nesse abastecimento é igual a:
a) R$ 2,35
b) R$ 2,38
c) R$ 2,40
d) R$ 2,43
e) R$ 2,46
Resolução
Basta calcularmos a média ponderada:
(30.2,90 + 20.1,80)/50 = (87 + 36)/50 = 123/50 = 2,46
Resposta: E
Gostou da prova resolvida do concurso PM ES 2013?
Deixe o seu comentário.
