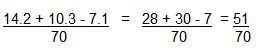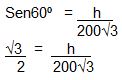Confira a prova resolvida do concurso para o Corpo de Bombeiros do estado do Acre (AC) realizado em 2012.
21. Calcule o valor da expressão [2 + 3 x 4] ÷ 7 + 7.
A) 9
B) 7
C) 4
D) 12
E) 1
[2 + 3 x 4] ÷ 7 + 7
[2 + 12] ÷ 7 + 7
14 ÷ 7 + 7
2 + 7
9
22. Sejam os conjuntos A = {1, 2, 3} e B = {2, 3, 5}, determine o conjunto A – B.
A) { }
B) {1, 5}
C) {5}
D) {1}
E) {2, 3}
O conjunto A – B é formado pelos elementos que pertencem a A e não pertencem a B, ou seja, A – B = {1}
23. Determine o valor de (n)/2, sabendo que é o número de divisores naturais de 3000.
A) 3
B) 4
C) 8
D) 16
E) 24
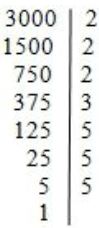
Fatorando:
3000 = 2.2.2.3.5.5.5
Para calcular o número de divisores, basta somar 1 a cada quantidade de números primos e multiplicar:
n = 4.2.4 = 32
n/2 = 16
24. Sabendo que A é uma matriz quadrada de ordem 3 e que o determinante de A é -2, calcule o valor do determinante da matriz 3A.
A) – 8
B) – 54
C) 27
D) 18
E) – 2
25. Determine o valor de x que provoca o valor máximo da função real f(x) = -x² + 7x – 10.
A) 3,5
B) – 2
C) 0
D) 10
E) – 1,5
Vamos achar as raízes pelo método de soma e produto:
a = -1, b = 7, c = -1
Soma = -b/a = -7/-1 = 7
Produto = -10/-1 = 10
Dois números cuja soma é 7 e o produto é 10. As raízes são 2 e 5.
O valor máximo (ou mínimo) é a média das raízes:
(2 + 5)/2 = 7/2 = 3,5
26. Determine o MDC (Maior Divisor Comum) e o MMC (Mínimo Múltiplo Comum), nesta ordem, dos números 60, 70 e 240.
A) 10 e 210
B) 30 e 210
C) 10 e 1680
D) 15 e 1680
E) 30 e 5040
Calculando o MDC:
Calculando o MMC:
27. Determine o produto das raízes da equação x² – 3x + 36 = 2x – x² – 14.
A) 2,5
B) 10
C) 25
D) 100
E) 50
x² – 3x + 36 = 2x – x² – 14.
x² – 3x + 36 – 2x + x² + 14 = 0
2x² – 5x + 50 = 0
Temos a = 2, b = -5, c = 50
Produto = c/a = 50/2 = 25
28. Determine o produto dos cinco primeiros números primos, quando dispostos em ordem crescente.
A) 2310
B) 720
C) 30030
D) 2520
E) 15015
2.3.5.7.11 = 2310
29. Determine o valor de (2/5) + (3/7) – (1/10).
A) 25/35
B) 51/70
C) 11/14
D) 17/20
E) 13/14
Temos que o mmc de 5, 7 e 10 é 70.
30. A medida do apótema de um hexágono regular cujo lado mede 200√3 cm corresponde a:
A) 100 cm
B) 168 cm
C) 150√3 cm
D) 200√3 cm
E) 300 cm
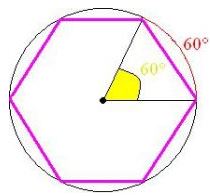
É fácil verificar pela figura que o hexágono pode ser dividigo em 6 triângulos equiláteros,
ou seja, todos os lados iguais e todos os ângulos iguais a 60º.
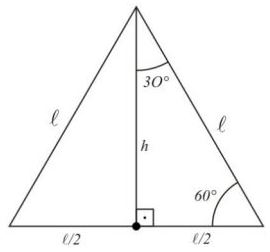
Em cada triângulo temos:
2h = 200.√3.√3
2h = 200.3
h = 600/2
h = 300
31. Considere o conjunto A = {1, 2, {3}} e assinale a alternativa que contém um sub conjunto de A.
A) {3}
B) {1, 3}
C) {2, 3}
D) {4, {3}}
E) {{3}}
Um subconjunto de A é um conjunto que só contém elementos de A.
A dificuldade está em saber que o número 3 não é um elemento de A, e sim o conjunto {3}, assim descartamos as letras a,b e c.
Claramente o 4 não pertence a A, logo descartamos também a letra d.
Nos resta a letra e, que como vimos, {3} pertence a A, logo {{3}} é subconjunto de A.
32. Determine o número que se obtém ao se escrever o número 3 no sistema de numeração de base 2.
A) (111)
B) (101)
C) (10)
D) (01)
E) (11)
Temos que 3 = 1.2 + 1.1
Logo, 3 na base 2 é 11
33. Sabendo que 2,5 Kg de farinha custam R$ 2,75, calcule quanto custarão 20 Kg da mesma farinha.
A) R$ 22,75
B) R$ 25,75
C) R$ 28,00
D) R$ 22,00
E) R$ 27,50
Vamos calcular o valor do quilo de farinha:
2,75/2,5 = 1,10
Logo, 20.1,10 = 22,00
34. Determine o aumento percentual aproximado sofrido pelo litro da gasolina, sabendo que custava R$ 2,80 e, que após o aumento, custa R$ 2,97.
A) 3%
B) 10%
C) 6%
D) 4%
E) 5%
Temos que a gasolina aumentou 0,17 reais.
Vamos calcular quanto isso representa sobre 2,80
0,17/2,80 = 0,06 = 6%
35. Determine a área de um retângulo cuja razão entre os lados é 2/3 e o perímetro é 100.
A) 300 u.a.
B) 150 u.a.
C) 600 u.a.
D) 450 u.a.
E) 750 u.a.
Sema seus lados x e y:
“ razão entre os lados é 2/3”
x/y = 2/3
2y = 3x
“o perímetro é 100”
2x + 2y = 100
Substituindo 2y por 3x na segunda equação:
2x + 3x = 100
5x = 100
x = 100/5
x = 20
Logo:
2y = 3x
2y = 3.20
2y = 60
y = 60/2
y = 30
Calculando a área:
x.y = 20.30 = 600