Confira aqui a prova resolvida do TRT ES (17), aplicada em 2013 pela CESPE.
Como sempre, a prova foi muito bem elaborada pela banca, que é uma das mais respeitadas do país.
Bom estudo!
Considerando a proposição P: “Se nesse jogo não há juiz, não há jogada fora da lei”, julgue os itens a, b, c seguintes, acerca da lógica sentencial.
Para analisarmos as afirmações a, b e c, vamos considerar:
P = ~Q → ~R
onde,
Q: Nesse jogo há juiz
R: Há jogada fora da lei
a) A negação da proposição P pode ser expressa por “Se nesse jogo há juiz, então há jogada fora da lei”.
Resolução
Para resolvermos a questão, basta sabermos que a negação de (A → B) é (~B → ~A)
Temos que ~(~Q → ~R) é equivalente a R → Q (Há jogada fora da lei então há juiz)
Resposta: ERRADO
b) A proposição P é equivalente a “Se há jogada fora da lei, então nesse jogo há juiz”.
Resolução
Pela questão anterior, A → B e ~B → ~A são equivalentes.
Resposta: CORRETO
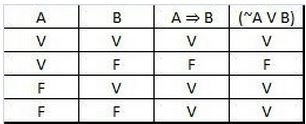
c) A proposição P é equivalente a “Nesse jogo há juiz ou não há jogada fora da lei”.
Resolução
Veja na tabela abaixo que A → B e ~A V B são equivalentes
Resposta: CORRETO
Considerando que, na fruteira da casa de Pedro, haja 10 uvas, 2 maçãs, 3 laranjas, 4 bananas e 1 abacaxi, julgue os próximos itens.
a) Há mais de 1.330 maneiras distintas de Pedro escolher pelo menos uma fruta entre aquelas que estão em sua fruteira.
Resolução
Pedro vai escolher algumas frutas. Ele tem a opção de pegar uma, duas ou várias.
Vamos analisar quantas opções ele tem para cada fruta:
- Uva: Pode pegar de 0 a 10, ou seja, 11 opções.
- Maçã: Pode pegar de 0 a 2, ou seja, 3 opções.
- Laranja: Pode pegar de 0 a 3, ou seja, 4 opções.
- Banana: Pode pegar de 0 a 4, ou seja, 5 opções.
- Abacaxi: Pode pegar 0 ou 1, ou seja, 2 opções.
Total de opções: 11 x 3 x 4 x 5 x 2 = 1320
Basta descontar a possibilidade de Pedro não pegar nenhuma fruta:
1320 – 1 = 1319
Há 1319 maneiras distintas, ou seja, menos de 1330.
Resposta: ERRADO
b) Se, para fazer uma salada de frutas, Pedro deve escolher pelo menos dois tipos de frutas, em qualquer quantidade, então há menos de 1.000 maneiras distintas de Pedro escolher frutas para compor sua salada.
Resolução
Na letra b vimos que ele tem 1319 opções para escolher pelo menos uma.
O que muda quando falamos em ‘pelo menos duas’ é que devemos descartar as opções que ele teria de escolher uma fruta apenas.
Para pegar apenas uva uma ele tem 10 opções. Apenas uma, apenas duas, apenas três, …, ou todas as 10 uvas.
Da mesma forma, duas opções pegando apenas maçãs, 3 para apenas laranjas, 4 para apenas bananas e uma para o abacaxi.
Total:
10 + 2 + 3 + 4 + 1 = 20 opções
Temos:
1319 – 20 = 1299 opções
Há 1299 maneiras distintas, ou seja, mais de 1000.
Resposta: ERRADO
c) Se Pedro desejar comer apenas bananas, haverá quatro maneiras de escolher algumas frutas para comer.
Resolução
Se ele quer apenas bananas, ele poderia pegar uma, duas, três ou quatro, ou seja, ele tem 4 opções.
Resposta: CERTO
Obs: A questão pode ter outra interpretação, repare que ele vai escolher algumas frutas, ou seja, poderíamos eliminar a opção de comer apenas uma banana e ter apenas 3 opções.
d) Se Pedro desejar comer apenas um tipo de fruta, a quantidade de maneiras de escolher frutas para comer será superior a 100.
Resolução
- Se ele comer apenas Uva ele terá 10 opções
- Se ele comer apenas Maçã ele terá 2 opções
- Se ele comer apenas Laranja ele terá 3 opções
- Se ele comer apenas Banana ele terá 4 opções
- Se ele comer apenas Abacaxi ele terá apenas 1 opção
Total de 20 opções, ou seja, inferior a 100.
Resposta: ERRADO
Considerando que dois álbuns de fotos, com x e y páginas, sejam montados com o menor número possível de capítulos — divisão das fotos por eventos — e que cada capítulo, nos dois álbuns, deva ter o mesmo número z de páginas, julgue os itens subsequentes.
a) Se x = 96 e y = 128, então z = 32.
Resolução
A questão pede para dividirmos dois álbuns na menor quantidade possível de capítulos com a mesma quantidade de páginas.
Se a quantidade de capítulos é a menor possível, a quantidade de páginas (z) por capítulo é a maior possível.
Repare que a quantidade de páginas é justamente o mdc de 96 e 128, ou seja, z = 32
Resposta: CORRETO
b) Se x é divisor de y, então z = x.
Resolução
Essa é uma das propriedades do mdc.
Se queremos calcular o mdc de dois números e um é múltiplo do outro, o mdc é o menor dos números.
Resposta: CORRETO
c) z é múltiplo de x.
Resolução
Repare que z é mdc de x e y.
Logo z não pode ser maior que x.
A única opção que teríamos para z ser múltiplo de x seria se x = z, que só ocorre quando x é divisor de y, que não é um dado fornecido pela questão.
Resolução: ERRADO
Gostou da resolução da prova do TRT ES 2013?
Deixe o seu comentário.