Confira aqui a prova resolvida do concurso para soldado da Polícia Militar do Estado do Piauí (PM – PI), realizado em 2017 pela NUCEPE.
Boa sorte!
Questão 15. Toda a produção semanal de latas de suco de certa fábrica foi vendida a três lojas, aqui designadas por A, B e C. Para a loja A, foi vendido um terço da produção, para a loja B, foi vendido 40% da produção, e, para a loja C, foram vendidas 11.360 unidades. Qual a produção semanal de latas de suco dessa fábrica?
A) 42.000 latas.
B) 42.300 latas.
C) 42.420 latas.
D) 42.540 latas.
E) 42.600 latas.
Resolução
Seja x a quantidade de latas produzidas na semana.
Temos que:
A loja A recebeu x/3 latas.
A loja B recebeu 0,4x latas.
A loja C recebeu 11360 latas.
x/3 + 0,4x + 11360 = x
3(x/3 + 0,4x + 11360) = 3.x
x + 1,2x + 34080 = 3x
34080 = 3x – x – 1,2x
0,8x = 34080
x = 34080/0,8
x = 42600
Resposta: E
Questão 16. Saindo da rodoviária de certa cidade, dois ônibus percorrem trajetos que só têm a rodoviária como ponto comum: um deles vai para o aeroporto, em percurso que leva 30 minutos, e o outro para a estação de metrô, em percurso que leva 24 minutos. Para cada um dos ônibus, os trajetos de ida e volta consomem o mesmo intervalo de tempo. Considerando as viagens de ida e volta, e supondo que os dois ônibus saem da rodoviária no mesmo instante, quanto tempo depois eles voltam a se encontrar, pela primeira vez, no ponto de partida?
A) 3 horas.
B) 4 horas.
C) 5 horas.
D) 6 horas.
E) 7 horas.
Resolução
Temos que nos atentar para o fato de que a questão deixa claro que os tempos de 30 e 24 minutos são apenas de ida, ou seja, os tempos de ida e volta são, respectivamente, 60 e 48 minutos.
O Ônibus 1 passará pela rodoviária a cada:
60, 120, 180…
O Ônibus 2 passará pela rodoviária a cada:
48, 96, 144…
Para calcularmos quando os ônibus se encontrarão, basta calcular o mínimo múltiplo comum de 48 e 60.
Temos que:
48 = 2⁴.3
60 = 2².3.5
MMC(48,60) = 2⁴.3.5 = 240
Daí, eles se encontrarão após 240 minutos (4 horas).
Resposta: B
Questão 17. Na tabela a seguir, temos o consumo mensal de água de uma família, durante os cinco primeiros meses de 2017.
Mês Consumo (em m³)
Janeiro 12,8
Fevereiro 13,5
Março 11,9
Abril 13,6
Maio 12,7
Se admitirmos que o preço do m³ de água é R$ 3,00, qual o valor médio, mensal, pago pelo consumo de água nessa família, nesses cinco meses?
A) R$ 38,40
B) R$ 38,50
C) R$ 38,60
D) R$ 38,70
E) R$ 38,80
Resolução
Calculando o consumo médio dos primeiros 5 meses de 2017:
M = (12,8 + 13,5 + 11,9 + 13,6 + 12,7)/5
M = 64,5/5
M = 12,9
Sabendo que cada m³ custa R$ 3,00:
12,9.3 = 38,7
Resposta: D
Questão 18. Em uma expedição militar, 25 pessoas planejam levar alimento suficiente para 16 dias, contando com 3 refeições por dia. Próximo à data marcada para o início da expedição, 5 pessoas resolvem se juntar ao grupo inicial para participar da expedição. Se eles fizessem apenas 2 refeições por dia, para quantos dias a comida planejada inicialmente seria suficiente?
A) 18 dias.
B) 19 dias.
C) 20 dias.
D) 21 dias.
E) 22 dias.
Resolução
Questão típica de regra de três composta, com três grandezas.
Pessoas Dias Refeições
25 16 3
30 x 2
↓ ↑ ↓
Observe que:
Quanto mais pessoas, menos dias com comida.
Quando mais dias, menos refeições por dia.
x/16 = 25/30 . 3/2
x/16 = 5/6 . 3/2
x/16 = 5/4
x = 20
Resposta: C
Questão 19. Maria comprou um computador em 3 parcelas mensais e iguais de R$ 540,80, a primeira parcela paga no momento da compra. Se o preço do computador à vista era de R$ 1500,00, e se foram cobrados juros compostos de 4% ao mês, quanto Maria pagou de juros (em valores do momento da compra)?
A) R$ 60,80
B) R$ 60,70
C) R$ 60,60
D) R$ 60,50
E) R$ 60,40
A questão deve ser anulada.
O valor à vista era de 1500.
Se considerarmos que Maria pagou a primeira parcela no momento da compra, o financiamento foi de:
1500 – 540,80 = 959,20
Neste caso, Maria financiou R$ 959,20 para pagar em duas parcelas mensais de R$ 540,80 (2 x 540,80 = 1081,60).
Trazendo todas as prestações para o tempo inicial:
PV = 540,80/1,04 + 540,80/1,04²
PV = 520 + 500
PV = 1020
Se a taxa fosse de 4% a.m., o valor de PV seria de 959,20.
Acho que a banca se confundiu quando trouxe todas as parcelas para a mesma data.
PV = 540,80 + 540,80/1,04 + 540,80/1,04²
PV = 540,80 + 520 + 500
PV = 1560,80
Neste caso a diferença foi exatamente de 60,80. Mas não está correto, pois se a taxa é realmente de 4% a.m., essa conta deveria ser igual ao valor financiado, ou seja, 1500.
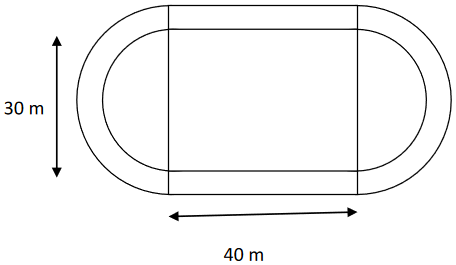
Questão 20. Uma praça é formada por um retângulo e dois semicírculos com diâmetros justapostos ao lado menor do retângulo. Os lados do retângulo medem 40 m e 30 m. Uma calçada com 3 m de largura deve ser construída em torno de uma praça. Qual o valor total a ser pago por essa calçada, se o metro quadrado do pavimento é de R$ 30,00? A seguir, temos uma ilustração da situação, fora de escala. Obs.: adote a aproximação π ≃ 3,14.
A) R$ 16.525,40
B) R$ 16.525,50
C) R$ 16.525,60
D) R$ 16.525,70
E) R$ 16.525,80
Resolução
Vamos calcular a área da calçada em duas etapas.
- No retângulo, temos 80 metros (40 + 40) de calçada:
80 x 3 = 240 m²
- Dois semicírculos geram um círculo completo. A área da calçada neste caso é a área da coroa circular representada pela diferença entre a área de uma circunferência de raio igual a 18 m e a área de uma circunferência de raio igual a 15 m.
π.18² – π.15² = π.(324 – 225) = 3,14.99 = 310,86 m²
Área total:
240 + 310,86 = 550,86 m²
Como cada m² custa 30 reais:
550,86 . 30 = 16.525,80
Resposta: E
Questão 21. Para cercar um terreno retangular, com uma cerca formada por 3 fios, foram usados 114 m de arame. Se o terreno tem área medindo 78 m2, em quantos metros a largura do terreno excede sua altura? Admita que a largura do terreno é maior que sua altura, ambas medidas em metros.
A) 6 m
B) 7 m
C) 8 m
D) 9 m
E) 10 m
Resolução
Se foram utilizados 114 m de arame em uma cerca formada por 3 fios, temos que o perímetro do terreno retangular é:
114 / 3 = 38 m
Sendo x a largura e y a altura do terreno:
2x + 2y = 38
x + y = 19
Como a área é igual a 78 m²:
x.y = 78
Resolvendo o sistema de equações:
x + y = 19
x.y = 78
É fácil perceber que os números são 13 e 6.
Como a questão informa que a largura é maior que a altura, a diferença será de:
13 – 6 = 7 m
Resposta: B
Gostou da prova resolvida do concurso para soldado da Polícia Militar do Piauí de 2017?
Curta e compartilhe nas redes sociais.
