Olá caro estudante. Confira aqui a prova resolvida do concurso para a PM do Espírito Santo (ES) realizado em 2013 pela Exatus, e que valeu vaga no curso de formação de oficiais (CFO).
Caso tenha alguma dúvida deixe o seu comentário em nosso Fórum e não se esqueça de compartilhar esta página nas redes sociais.
Bom estudo!
Questão 61. Numa cerimônia militar, os soldados de um quartel da capital capixaba foram organizados em fileiras. Na primeira fileira havia 18 soldados, na segunda 20 soldados, na terceira 22 soldados e assim sucessivamente. Sabe-se que no total havia 480 soldados nessa cerimônia. O número de fileiras de soldados que foram formadas nessa cerimônia é igual a:
a) 13
b) 14
c) 15
d) 16
e) 17
Resolução
Nota-se que temos uma P.A., onde o primeiro termo é o 18, a razão é o 2 e a soma dos termos é 480.
Pela fórmula do termo geral:
an = a1 + (n – 1)r
an = 18 + (n – 1)2
an = 18 + 2n – 2
an = 16 + 2n
Vamos agora substituir na fórmula da soma dos termos de uma P.A.
Sn = (a1 + an).n/2
480 = (18 + 16 + 2n).n/2
480.2 = (34 + 2n)n
960 = 34n + 2n²
2n² + 34n – 960 = 0
n² + 17n – 480 = 0
Temos uma equação do segundo grau.
Resolvendo pelo método de soma e produto:
Soma = -b/a = -17
Produto = c/a = -480
Os dois números cuja soma é -17 e o produto é -480 são -32 e 15.
Como o n representa a quantidade de termos, os valores negativos não servem, logo, n = 15.
Resposta: C
Questão 62. O soldado Ryan reside no 13 andar de um prédio de 15 andares. Sabe-se a distância entre o piso do andar onde mora o soldado Ryan e o piso térreo é de 39 m. Uma pessoa com altura de 1,8 m na parada ao lado desse edifício projeta uma sombra de 30 cm. Neste mesmo instante, a sombra projetada pelo edifício onde mora o soldado Ryan é igual a:
a) 13
b) 14
c) 10
d) 16
e) 8
Resolução
Temos que Ryan mora no 13º andar e que a distância do seu piso até o piso térreo é de 39 metros.
Considerando que cada andar é da mesma altura, temos 12 andares mais o térreo, ou seja, 13 pavimentos.
Se são 39 metros, e 13 pavimentos, cada pavimento mede 3 metros de altura. Somando-se as alturas dos andares 13, 14 e 15, temos que o edifício mede 48 metros.
Sabendo que o sol forma o mesmo angulo com o prédio e com a pessoa, podemos calcular usando semelhança de triângulos. Veja a figura:
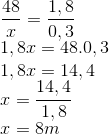Resposta: E
Questão 63. Duas torneiras estão instaladas em um reservatório com capacidade para 6 metros cúbicos de água. Uma é capaz de encher o reservatório em 2 horas, e a outra o faz em 4 horas. Se abertas simultaneamente, em uma hora, as duas torneiras terão despejado no tanque (em 1 metro cúbico cabem 1000 litros):
a) 1300
b) 4000
c) 1000
d) 4500
e) 5000
Resolução
A torneira que enche em duas horas, em uma hora encherá a metade, ou seja, 3000 litros.
A torneira que enche em 4 horas, em uma hora encherá 1/4, ou seja, 1500 litros.
Total = 3000 + 1500 = 4500
Resposta: D
Questão 64. Um caneco em formato de hemisfério cujo raio interno mede 20 cm é utilizado para transferir água de outro recipiente maior para copos em formato de cilindro circular reto, com raio da base medindo 4 cm e altura 15 cm. Considerando que esse caneco esteja com água equivalente a 4/5 do seu volume máximo, a água contida nele é suficiente para encher:
a) 13
b) 14
c) 10
d) 16
e) 17
Resolução
Vamos calcular todos os volumes em centímetros cúbicos:
Volume do copo em formato de hemisfério:
Como ele tem formato de hemisfério, basta calcular o volume de uma esfera e dividir por 2:
Volume da esfera: V = π.r³.4/3 = π.20³.4/3 = 32000π/3
Volume do copo = 32000π/3 / 2 = 16000π/3
O problema nos fala que o copo estava com 4/5 da capacidade:
16000π/3 x 4/5 = 12800.π/3
Volume dos copos em formato de cilindro:
Volume do cilindro = altura x π.r² = 15.π.4² = 240π
Dividindo os dois volumes, o π é cancelado e temos 17,7777 copos
Resposta: E
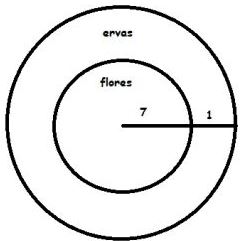
Questão 65. Adriana planta flores num canteiro circular de raio 8 m. Ao redor desse canteiro, ela pretende plantar ervas medicinais formando uma coroa circular, de maneira que a parte destinada às flores sofrerá uma redução de 2 m em seu diâmetro. A área ocupada pelas ervas medicinais neste canteiro será igual a:
a) 13π
b) 14π
c) 15π
d) 16π
e) 8π
Resolução
Adriana plantava em um circulo de raio 8. Como ela vai plantar ervas medicinais em volta, reduzindo em 2m o diâmetro, o raio passará a ser 7.
Assim, a área da coroa circular será a diferença entre a área do circulo de raio 8 e do circulo de raio 7 (Área circunferência = π.r²):
π.8² – π.7² = 64π – 49π = 15π
Resposta: C
Questão 66. O Soldado Fontes possui 3 pares de sapatos, 4 camisas e 3 calças que fazem parte do uniforme de gala da Polícia Militar. Para comparecer a um evento sobre segurança pública trajando um uniforme de gala, o soldado Fontes pode se vestir de:
a) 33
b) 34
c) 40
d) 36
e) 37
Resolução
Fontes tem:
3 opções para o sapato
4 opções para a camisa
3 opções para a calça
Total = 3 x 4 x 3 = 36 opções
Resposta: D
Questão 67. A largura, a altura e o comprimento de um paralelepípedo reto retângulo formam, nessa ordem, uma progressão geométrica de razão 3. Sabe-se que o volume desse paralelepípedo é igual a 5,832 litros. A altura desse paralelepípedo mede:
a) 1,3 m
b) 1 m
c) 0,10 m
d) 0,16 m
e) 0,18 m
Resolução
Se em 1 metro cúbico temos 1000 litros, para termos 5,832 litros precisamos ter 0,005832 metros cúbicos.
Sabemos que o volume do paralelepípedo é dado pela fórmula: V = largura x altura x comprimento.
Como os lados formam uma PG de razão 3, temos:
Largura = x/3
Altura = x
Comprimento = 3x
Assim,
x/3 . x . 3x = 0,005832
x³ = 0,005832
x = 0,18 m
Resposta: E
Questão 68. Uma agência de viagens vende pacote turísticos coletivos com destino a Fortaleza. Um pacote para 40 clientes custa R$ 2000,00 por pessoa e, em caso de desistência, cada pessoa que permanecer no grupo deve pagar mais R$ 100,00 por cada desistente do pacote de viagem. Dessa forma, para que essa agência obtenha lucro máximo na venda desse pacote de viagens, o número de pessoas que devem realizar a viagem é igual a:
a) 33
b) 34
c) 30
d) 29
e) 32
Resolução
Repare que o preço total é dado pela quantidade de pessoas vezes o preço por pessoa, que é 2000 mais 100 por desistente.
C(x) = x(2000 + 100(40 – x))
C(x) = x(2000 + 4000 – 100x)
C(x) = x(6000 – 100x)
C(x) = 6000x – 100x²
Temos uma função do segundo grau.
Vamos calcular as raízes:
6000x – 100x² = 0
60x – x² = 0
x(60 – x) = 0
Assim, x = 0 ou x = 60
Como em nossa função o valor de a = -100 < 0, o gráfico é uma parábola para baixo, portanto possui valor máximo, e é exatamente o valor entre as raízes 0 e 60, portanto o valor máximo ocorre quando x = 30.
Resposta: C
Questão 69. Alberto aplicou um capital de R$ 4160,00 à taxa de juros simples de 15% a.a. por um período suficiente para que o montante a ser retirado seja o triplo do capital aplicado. Dessa forma, o período de aplicação desse capital é:
a) 13 anos e 4 meses
b) 13 anos e 5 meses
c) 13 anos e 6 meses
d) 13 anos e 7 meses
e) 13 anos e 8 meses
Resolução
Para que o dinheiro retirado seja o triplo do aplicado, este deve crescer 200%.
Como temos o regime de juros simples, basta dividirmos 200% por 15%/ano, que é igual a 13,333… anos.
Note que 0,3333… = 1/3 = 4 meses.
Prazo total: 13 anos e 4 meses
Resposta: A
Questão 70. Dadas as retas r e s, determinadas respectivamente pelas equações 2x + y = 3 e 3x – 4y = -23, é correto afirmar que r e s são retas:
a) concorrentes
b) paralelas
c) congruentes
d) adjacentes
e) relacionadas
Resolução
Vamos descobrir se as retas têm pontos em comum, para isto, devemos substituir uma reta na outra, conforme abaixo:
Na equação da reta r temos:
y = 3 – 2x
Substituindo na equação da reta s:
3x – 4(3 – 2x) = -23
3x – 4.3 + 4.2x = -23
3x + 8x – 12 = -23
11x = -23 + 12
11x = -11
x = -11/11 = -1
Voltando a equação da reta r, agora com o valor de x = -1:
y = 3 – 2x = 3 – 2(-1) = 3 + 2 = 5
Assim, o ponto em comum é (-1, 5) e as retas são concorrentes.
Resposta: A
Questão 71. Donato, patrulheiro militar, utiliza uma bicicleta no exercício da sua função, que é patrulhar uma região turística de Vitória-ES. Sabe-se que o pneu dessa bicicleta possui formato circular de diâmetro medindo 70 cm. Considerando que na última quinta-feira Donato percorreu 21,4 km com essa bicicleta em serviço de patrulhamento, é correto afirmar que o pneu dessa bicicleta deu: (Dado π= 3)
a) 10000 voltas
b) 10190 voltas
c) 10199 voltas
d) 10210 voltas
e) 10220 voltas
Resolução
Vamos primeiro calcular quanto o patrulheiro anda após uma volta do pneu:
Pela fórmula do comprimento de uma circunferência:
C = 2.π.r = 2.3.35 = 210 cm = 2,1 metros
Repare que usamos r = 35 cm pois o diâmetro da roda é 70 cm.
Temos que 21,4 km equivalem a 21400 metros.
Como em uma volta ele anda 2,1 metros, e no total ele andou 21400 metros, basta efetuar a divisão:
21400/2,1 = 10190,4 voltas
Resposta: B
Questão 72. Acerca das posições relativas entre retas no espaço, analise as seguintes afirmações:
I- Por um ponto da reta r pode-se traçar infinitas retas perpendiculares à reta r.
Item verdadeiro. Basta desenhar uma reta r e uma reta s perpendicular a r. Agora imagine uma rotação de s em relação a r. Teremos infinitas retas, todas perpendiculares a r.
II- Por um ponto situado fora de uma reta, existe uma reta paralela à reta dada.
Item verdadeiro. Dada uma reta e um ponto, sempre é possível traçarmos uma paralela a reta e passando pelo ponto.
III- Três retas que, duas a duas, não têm ponto em comum são ditas retas reversas.
Item falso. Dizemos que duas retas são reversas quando não pertencerem a um mesmo plano e não forem paralelas entre si. Portanto informação da questão não condiz com a definição.
IV- Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si.
Item falso. Elas podem ser paralelas a um plano, mas não pertencerem a um mesmo plano.
V- Três retas concorrentes num mesmo ponto são coplanares.
Item falso. É fácil desenhar em uma folha duas retas concorrentes, que serão coplanares, agora imagine uma outra reta concorrente no mesmo ponto, porém perfurando a folha.
Questão 73. Otávio, Major da Polícia Militar, está a 1500 dias de tornar-se um militar da reserva. Considerando que hoje é domingo, o último dia de trabalho de Otávio será uma:
a) segunda feira
b) terça feira
c) quarta feira
d) quinta feira
e) sexta feira
Resolução
Como uma semana possui 7 dias, dividindo 1500 por 7, temos 214 e resto 2.
Sabendo disto, Otávio trabalhará mais 214 semanas e 2 dias. Se hoje é domingo, mais dois dias temos terça-feira.
Resposta: B
Questão 74. Sejam x e y os catetos de um triângulo retângulo cuja área mede 60 cm². Se x e y são múltiplos de 2 e 3, respectivamente, então o semiperímetro desse triângulo mede:
QUESTÃO ANULADA
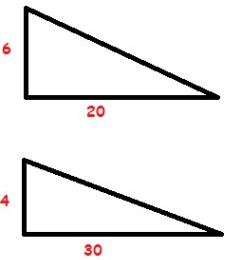
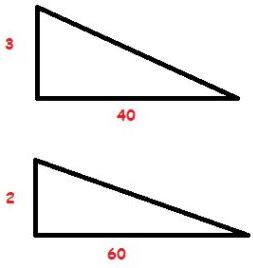
Não existe apenas uma solução para o problema. Veja abaixo que existem vários triângulos de área 60 e de catetos múltiplos de 2 e 3.
Questão 75. O volume do sólido gerado pela rotação de um triângulo isósceles de lados congruentes medindo 5 cm e base medindo 6 cm, em torno da base é igual a:
a) 12π cm³
b) 13π cm³
c) 14π cm³
d) 15π cm³
e) 16π cm³
Resolução
Veja na figura que após a rotação em torno da base, teremos um sólido formado por dois cones iguais. Basta então calcular o volume de um deles e multiplicar por 2.
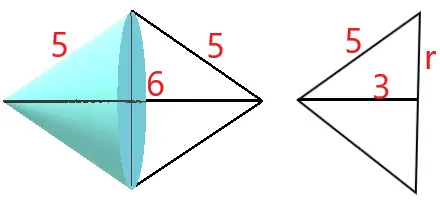
Primeiramente vamos calcular o raio do cone através do Teorema de Pitágoras, conforme figura:
5² = 3² + r²
r² = 25 – 9
r² = 16
r = 4
Calculando o volume do cone:
V = Área da base x altura / 3
V = π x 4² x 3 / 3
V = π x 16
V = 16π cm³
Volume total:
2 . 16π = 32π cm³
Resposta: E
Questão 76. Sendo “S” denominada de área do polígono determinado pelas coordenadas cartesianas dos pontos A(5,0), B(2,3), C(1,0) e D(6,5), é correto afirmar que a área desse polígono é:
a) 13
b) 14
c) 15
d) 16
e) 17
Resolução
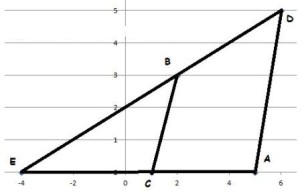
Marcando os pontos no plano cartesiano, podemos ver o formato do polígono ABCD:
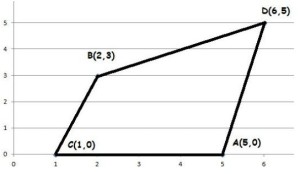
Para resolver a questão vamos alongar o lado BD até o eixo x, encontrando o ponto E (-4, 0), veja figura.
Veja que a área procurada é a diferença das áreas dos triângulos AED e EBC.
Área do triângulo AED:
A = 9×5/2 = 45/2 = 22,5
Área do triângulo EBC:
A = 5×3/2 = 15/2 = 7,5
Temos então 22,5 – 7,5 = 15
Resposta: C
Questão 77. O Espírito Santo vem presenciando, nos últimos 20 anos, um considerável crescimento nos índices de criminalidade e violência. Em 2005, foram 50,6 homicídios por 100 mil habitantes, um aumento de 161% quando comparado à taxa de 19,4 ocorridos duas décadas antes. Para contrapor esse cenário, o ES em ação criou o CT03 – Comitê Temático de Redução da Violência e da Criminalidade, que possui o objetivo de contribuir para que, até 2025, o Estado reduza a taxa de homicídios para valores inferiores a 10 por 100 mil habitantes. A redução da criminalidade aos níveis pretendidos pelo CT03 implica que a queda na taxa de homicídios de 2005 para 2025 deve ser de:
a) 60%
b) 65%
c) 70%
d) 75%
e) 80%
Resolução
O objetivo é sair de 50,6 por 100 mil para 10 por 100 mil.
Como 10 é aproximadamente 20% de 50,6, a taxa de homicídios deve cair aproximadamente 80%.
Resposta: E
Questão 78. A tabela que segue é demonstrativa do levantamento realizado por determinado batalhão de Polícia Militar, no que se refere às idades dos policiais integrantes do grupo especial desse batalhão:
Idade Nr. de Policiais
25——-12
28——-15
30——-25
33——-15
35——-10
40——–8
A moda, média e mediana dessa distribuição são, respectivamente, iguais a:
a) 30, 31, 30
b) 31, 31, 30
c) 30, 31, 31
d) 30, 30, 30
e) 31, 30, 31
Resolução
Moda é o valor que aparece com mais frequência: 30.
Média: Temos que somar todas as idades e dividir pela quantidade de policiais:
(25×12 + 28×15 + 30×25 + 33×15 + 35×10 + 40×8)/85
= (300 + 420 + 750 + 495 + 350 + 320)/85
= 2635/85 = 31
Mediana é o termo do meio quando colocamos todos em ordem:
São 85 termos, o do meio é o termo de número 43, ou seja, 30 anos.
Resposta: A
