Quer trabalhar na maior empresa de petróleo do país? Confira aqui a prova resolvida do concurso para a Petrobras, realizado em 2017 pela Cesgranrio, para o cargo de técnico de operações júnior.
Veja na sessão provas resolvidas a resolução referente a outros concursos.
Bom estudo!
Questão 11. Os conjuntos P e Q têm p e q elementos, respectivamente, com p + q = 13. Sabendo-se que a razão entre o número de subconjuntos de P e o número de subconjuntos de Q é 32, quanto vale o produto pq?
(A) 16
(B) 32
(C) 36
(D) 42
(E) 46
Resolução
Clique aqui para assistir a resolução no YouTube.
A fórmula utilizada para calcular a quantidade de subconjuntos de um conjunto com n elementos é a seguinte:
q = 2n
Onde:
q é a quantidade de subconjuntos
n é a quantidade de elementos
Pela fórmula, temos que:
- o conjunto P possui 2p subconjuntos
- o conjunto Q possui 2q subconjuntos
Sabendo que a razão entre o número de subconjuntos de P e o número de subconjuntos de Q é 32:
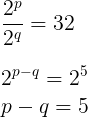
O enunciado também informa que p + q = 13. Basta então resolver o seguinte sistema de equações:
p + q = 13
p – q = 5
Somando as equações:
p + q + p – q = 13 + 5
2p = 18
p = 9
Calculando o valor de q:
p + q = 13
9 + q = 13
q = 13 – 9
q = 4
Calculando o produto pq:
p.q = 9.4 = 36
Resposta: C
Questão 12. Qual o maior valor de k na equação log(kx) = 2log(x+3) para que ela tenha exatamente uma raiz?
(A) 0
(B) 3
(C) 6
(D) 9
(E) 12
Resolução
log(kx) = 2log(x+3)
Aplicando a propriedade do logaritmo de potências:
log(kx) = log(x+3)²
kx = (x+3)²
kx = x² + 6x + 9
x² + 6x – kx + 9 = 0
x² + (6 – k)x + 9 = 0
Calculando o valor de Delta na equação do segundo grau:
Δ = b² – 4ac
Δ = (6 – k)² – 4.1.9
Δ = 36 – 12k + k² – 36
Δ = k² – 12k
Como sabemos, uma equação do segundo grau possui apenas uma raiz quando Δ = 0. Vamos calcular para quais valores de k isto acontece.
k² – 12k = 0
k(k – 12) = 0
k = 0 ou k = 12
Veja que a equação possui apenas uma raiz quando k = 0 ou k = 12. Como a questão pede o menor valor, temos que k = 12.
Resposta: E
Questão 13. Quantos valores reais de x fazem com que a expressão abaixo assuma o valor de 1?
![]()
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
Resolução
A expressão pode assumir o valor de 1 em 2 casos distintos:
- expoente igual a zero, pois “todo número diferente de zero elevado a zero é igual a 1”;
- base igual a 1;
- base igual a -1 e expoente par.
Caso 1.
Vamos procurar os valores de x que fazem com que o expoente seja igual a zero.
x² + 4x – 60 = 0
Calculando o valor de Δ:
Δ = b² – 4.a.c
Δ = 4² – 4 . 1 .(-60)
Δ = 16 + 240
Δ = 256
Aplicando a fórmula de Bhaskara:
x = (-b +- √Δ)/2a
x = (-4 +- √256)/2.1
x = (-4 +- 16)/2
x’ = 12/2 = 6
x” = -20/2 = -10
Caso 2
Vamos procurar os valores de x que fazem a base ser igual a 1.
x² – 5x + 5 = 1
x² – 5x + 5 – 1 = 0
x² – 5x + 4 = 0
Calculando o valor de Δ:
Δ = b² – 4.a.c
Δ = (-5)2 – 4.1.4
Δ = 25 – 16
Δ = 9
Aplicando Bhaskara:
x = (-b +- √Δ)/2a
x = (-(-5) +- √9)/2.1
x = (5 +- 3)/2
x’ = 8/2 = 4
x” = 2/2 = 1
Caso 3
Vamos procurar os valores de x que fazem a base ser igual a -1.
x² – 5x + 5 = -1
x² – 5x + 5 + 1 = 0
x² – 5x + 6 = 0
Calculando o valor de Δ:
Δ = b² – 4.a.c
Δ = (-5)² – 4 . 1 . 6
Δ = 25 – 24
Δ = 1
Aplicando Bhaskara:
x = (-b +- √Δ)/2a
x = (-(-5) + √1)/2.1
x = (5 +- 1)/2
x’ = 6/2 = 3
x” = 4/2 = 2
Basta agora verificar se os expoentes serão pares em algum desses dois casos.
- Para x = 2
x² + 4x – 60
2² + 4.2 – 60
4 + 8 – 60
-48 (par)
- Para x = 3
x² + 4x – 60
3² + 4.3 – 60
9 + 12 – 60
-39 (ímpar)
Assim, existem 5 valores de x que fazem a expressão assumir o valor numérico 1:
-10, 1, 2, 4 e 6
Resposta: D
Questão 14. Uma loja de departamento colocou 11 calças distintas em uma prateleira de promoção, sendo 3 calças de R$ 50,00, 4 calças de R$ 100,00 e 4 calças de R$ 200,00. Um freguês vai comprar exatamente três dessas calças gastando, no máximo, R$ 400,00. De quantos modos diferentes ele pode efetuar a compra?
(A) 46
(B) 96
(C) 110
(D) 119
(E) 165
Resolução
O freguês irá comprar 3 calças, onde tanto faz a ordem, ou seja, temos uma combinação de 11 elementos, tomados 3 a 3. O único problema é que temos algumas restrições, pois a compra não pode ultrapassar o valor total de 400 reais.
Resolveremos a questão calculando a quantidade possível de combinações, e descartando os casos onde o valor passaria de 400 reais.
- Quantidade total de combinações
C11,3 = 11! / 3!.(11-3)!
C11,3 = 11! / 3!.8!
C11,3 = 165
- Quantidade de combinações com 3 calças de 200 reais
C4,3 = 4!/3!.(4-3)!
C4,3 = 4!/3!.1!
C4,3 = 4
- Quantidade de combinações com 2 calças de 200 reais e qualquer uma das outras 7 de 50 ou 100 reais
7.C4,2 = 7.4!/2!.(4-2)!
7.C4,2 = 7.4!/2!.2!
7.C4,2 = 7.6
7.C4,2 = 42
Total:
165 – 4 – 42 = 119
Resposta: D
Questão 15. A soma dos n primeiros termos de uma progressão geométrica é dada por
![]()
Quanto vale o quarto termo dessa progressão geométrica?
(A) 1
(B) 3
(C) 27
(D) 39
(E) 40
Podemos achar o quarto termo da PG subtraindo a soma dos quatro primeiros termos pela soma dos três primeiros termos.
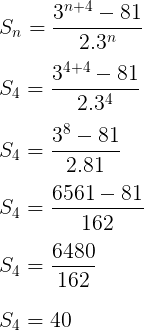
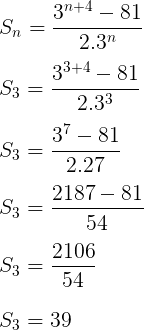
S4 – S3 = 40 – 39 = 1
Resposta: A
Questão 16. Na matriz abaixo, m, n e p são números inteiros ímpares consecutivos tais que m < n < p.
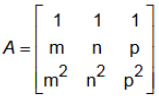
Qual é o valor da expressão abaixo?
![]()
(A) 2
(B) 8
(C) 16
(D) 20
(E) 22
Analisando a construção da matriz e as propriedades dos determinantes, podemos escolher quaisquer valores para m, n e p, que o valor de detA não será alterado.
Sejam:
m = 1
n = 3
p = 5
Veja como ficará a nossa matriz A:
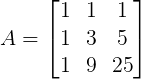
Calculando detA:
detA = 1.3.25 + 1.5.1 + 1.1.9 – 1.3.1 – 9.5.1 – 25.1.1
detA = 75 + 5 + 9 – 3 – 45 – 25
detA = 16
Concluindo:
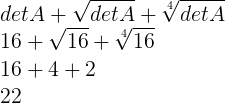
Resposta: E
Questão 17. A Figura a seguir mostra um cilindro reto, um cone reto e uma esfera que tangencia a base do cilindro e as geratrizes do cilindro e do cone. O cone e o cilindro têm como base um círculo de raio 7 cm e a mesma altura que mede 24 cm.
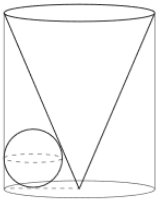
Qual o volume, em centímetros cúbicos, da região interior ao cilindro e exterior à esfera e ao cone?
(A) 800π
(B) 784π
(C) 748π
(D) 684π
(E) 648π
Resolução
O volume da região interior ao cilindro e exterior à esfera e ao cone é justamente o volume do cilindro, subtraído dos volumes do cilindro e da esfera. Veja:
V(cone) – V(cilindro) – V(esfera)
As fórmulas de volume do cilindro e do cone dependem apenas do raio e da altura, e essas informações já foram dadas pela banca. A maior dificuldade é em relação à esfera, da qual não sabemos a medida do raio. Esse será o nosso objetivo inicial.
Utilizando as informações apresentadas no enunciado, podemos desenhar um triângulo retângulo ABC, cujos catetos medem 24 cm (altura do cilindro) e 7 cm (raio da base do cilindro). A medida hipotenusa AC pode ser calculada através do teorema de Pitágoras.
AC² = AB² + BC²
AC² = 24² + 7²
AC² = 576 + 49
AC² = 625
AC = √625
AC = 25 cm
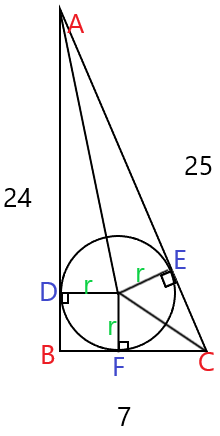
Na figura, D, E e F são os pontos de tangencia da circunferência de centro O.
BF = r ⇒ FC = 7-r ⇒ EC = 7-r
BD = r ⇒ AD = 24-r ⇒ AE = 24-r
Como AE + EC = AC = 25:
24 – r + 7 – r = 25
31 – 2r = 25
2r = 31 – 25
2r = 6
r = 3 cm
- Calculando o volume do cilindro de raio 7 e altura 24:
V = Área da base x altura
V = π.7².24
V = 1176π
- Calculando o volume do cone de raio 7 e altura 24:
V = Área da base x altura / 3
V = π.7².24/3
V = 392π
- Calculando o volume da esfera de raio 3:
V = (4/3).π.r³
V = (4/3).π.3³
V = 36π
Finalizando:
1176π – 392π – 36π = 748π
Resposta: C
Questão 18. Um arame de extremidades C e D e 8 cm de comprimento é dobrado de modo a formar um triângulo equilátero ABC mantendo os pontos B, C e D alinhados, conforme a Figura a seguir.
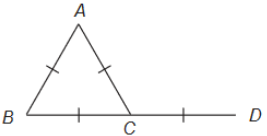
Qual a distância, em centímetros, entre os pontos A e D?
(A) √3
(B) 2√3
(C) 4√3
(D) 2
(E) 4
Resolução
Podemos resolver a questão traçando a reta AD e “brincando” com os ângulos dos triângulos.
Como o arame mede 8 cm, AC = AB = BC = CD = 2 cm.
Como ABC é um triângulo equilátero, cada ângulo interno mede 60º, de onde podemos concluir que o ângulo externo mede 120º.
Observando que DCA é um triângulo isósceles, podemos concluir que os ângulos internos A e D medem 30º. Daí, o triângulo ABD é retângulo em A.
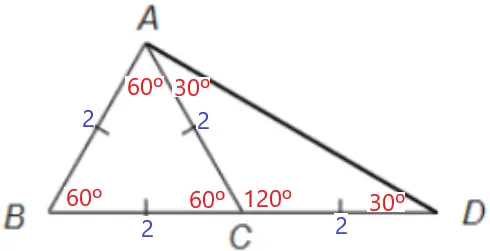
Utilizando o teorema de Pitágoras para calcular o valor do cateto AD:
BD² = AB² + AD²
4² = 2² + AD²
16 = 4 + AD²
AD² = 16 – 4
AD² = 12
AD = √12
AD = 2.√3
Resposta: B
Questão 19. Qual a equação reduzida da reta que contém a altura relativa ao lado BC do triângulo ABC, onde A, B e C são os pontos (3, 4), (1, 1) e (6, 0), respectivamente?
(A) y = 5x – 11
(B) y = 6x – 11
(C) y = – 5x + 11
(D) y = – 6x – 11
(E) y = 5x + 11
Temos na figura abaixo o triângulo ABC e a reta (verde) que representa a altura relativa ao lado BC.
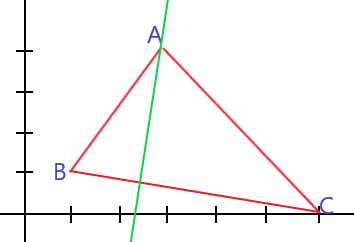
Calculando o coeficiente angular (m1) de BC:
m1 = (yc – yb)/(xc – xb)
m1 = (0 – 1)/(6 – 1)
m1 = -1/5
Sabendo que a altura é perpendicular a BC, podemos calcular o seu coeficiente angular (m2) através da seguinte relação:
m1.m2 = -1
-1/5.m2 = -1
m2 = 5
Agora que sabemos o coeficiente angular da altura relativa a BC, a equação reduzida será da seguinte forma:
y = 5.x + n, onde n é o coeficiente angular.
Veja que a altura passa pelo vértice A, ou seja, o ponto (3,4) pertence à altura. Substituindo os valores de x e y:
y = 5.x + n
4 = 5.3 + n
4 = 15 + n
n = 4 – 15
n = -11
Daí, a equação reduzida da altura relativa a BC é:
y = 5.x – 11
Resposta: A
Questão 20. Um feirante sabe que consegue vender seus produtos a preços mais caros, conforme o horário da feira, mas, na última hora, ele deve vender suas frutas pela metade do preço inicial. Inicialmente, ele vende o lote de uma fruta a R$ 10,00. Passado algum tempo, aumenta em 25% o preço das frutas. Passado mais algum tempo, o novo preço sofreu um aumento de 20%. Na última hora da feira, o lote da fruta custa R$ 5,00. O desconto, em reais, que ele deve dar sobre o preço mais alto para atingir o preço da última hora da feira deve ser de
(A) 12,50
(B) 10,00
(C) 7,50
(D) 5,00
(E) 2,50
Resolução
Clique aqui para assistir a resolução da questão no YouTube.
Preço inicial: R$ 10,00
Preço após os dois aumentos:
10 . 1,25 . 1,20 = 15
Se na última hora da feira o lote da fruta custa 5 reais, o desconto final foi de 10 reais.
Resposta: B
Ufaaaaaaaaaaaa!
Você conferiu a resolução da prova da Petrobras 2017, cargo de técnico de operação júnior.
A Cesgranrio caprichou na prova. Realmente não estava fácil. Os candidatos foram bem exigidos!
Boa sorte a todos e fiquem com Deus!

Muito interessante mesmo! Continue com o bom trabalho!
Adorei vou recomendar pra todos que conheço. 🙂
Obrigado Ines!
Sua opinião é muito importante para nós.
Volte sempre que precisar.