Quer conferir a prova resolvida do concurso para Técnico do INSS de 2016? Chegou ao site certo.
Veja a resolução da prova de matemática e raciocínio lógico realizada hoje a tarde.
Boa sorte a todos!
Art. 21. A alíquota de contribuição dos segurados contribuinte individual e facultativo será de vinte por cento sobre o respectivo salário-de-contribuição.
Considerando o art. 21 da Lei n. 8.212/1991, acima reproduzido, julgue o item seguinte.
45 – Se o valor da contribuição de um segurado contribuinte individual for superior a R$700,00, então o salário-de-contribuição desse indivíduo é superior a R$3.500,00.
Comentário:
Vamos considerar um segurado que contribui com R$ 700,00.
É fácil verificar que 20% de R$ 3.500,00 é igual a R$ 700,00. Logo, quem recolhe um valor superior a R$ 700,00, logicamente ganha um valor superior a R$ 3.500,00.
Resposta: Certo.
46 – Para quaisquer proposições p e q, com valores lógicos quaisquer, a condicional p⇒(q⇒p) será, sempre, uma tautologia.
Comentário:
Dizemos que uma fórmula proposicional é uma tautologia quando é verdadeira para todas as opções.
Vamos então montar a tabela verdade e analisar todos os casos:
| p | q | q⇒p | p⇒(q⇒p) |
| V | V | V | V |
| V | F | V | V |
| F | V | F | V |
| F | F | V | V |
Veja que em todos os casos possíveis temos que p⇒(q⇒p) é uma verdade, logo é uma tautologia.
Resposta: Certo.
47 – Caso a proposição simples “Aposentados são idosos” tenha valor lógico falso, então o valor lógico da proposição “Aposentados são idosos, logo eles devem repousar” será falso.
Comentário:
Sejam:
A: Aposentados são idosos
B: eles devem repousar
Vamos montar a tabela verdade:
| A | B | A⇒B |
| V | V | V |
| V | F | F |
| F | F | V |
| F | V | V |
A questão afirma que A⇒B é falso quando A também é falso.
Observando a tabela verdade, temos claramente que quando A é falso, A⇒B só pode ser verdadeiro.
Resposta: Errado
48 – Dadas as proposições simples p: “Sou aposentado” e q: “Nunca faltei ao trabalho”, a proposição composta “Se sou aposentado e nunca faltei ao trabalho, então não sou aposentado” deverá ser escrita na forma (p∧q)⇒~p, usando-se os conectivos lógicos.
Comentário:
Sejam:
p = “sou aposentado”
q = “nunca faltei ao trabalho”
~p = “não sou aposentado”
E considerando que utilizamos o símbolo ∧ para o conectivo “e”, e também o símbolo ⇒ para o conectivo “implica” ou “então”, temos claramente que a representação está correta.
Resposta: Certo.
49 – A sentença “Bruna, acesse a internet e verifique a data de aposentadoria do Sr. Carlos!” é uma proposição composta que pode ser escrita na forma p∧q.
Comentário:
A questão deve ter confundido muitos candidatos pois o conectivo e está representado corretamente. O que não está correto é que não temos proposições. Não existem afirmações e sim ordens.
Resposta: Errado
50 – Se A, B e C forem conjuntos quaisquer tais que A, B ⊂ C, então (C\A) ∩ (AUB) = (C∩B).
Comentário:
Utilizando a informação que os conjuntos A e B estão contidos no conjunto C, temos a seguinte figura:
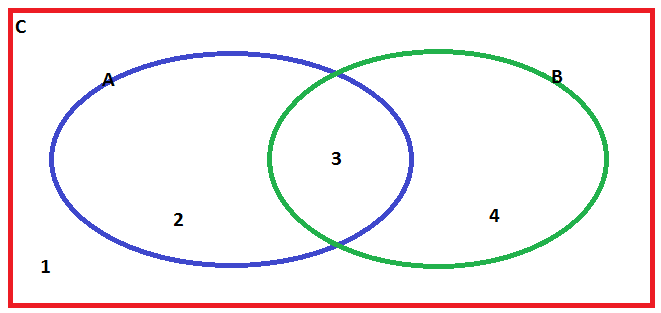
Repare que a figura tem 4 regiões:
1 – Elementos que pertencem a C mas não pertencem nem a A nem a B.
2- Elementos que pertencem a A mas não pertencem a B.
3- Elementos que pertencem a A e B ao mesmo tempo.
4- Elementos que pertencem a B mas não pertencem a A.
Vamos analisar se a afirmação (C\A) ∩ (AUB) = (C∩B) é verdadeira:
C\A é o conjunto dos elementos que pertencem a C mas não pertencem a A:
Regiões 1 e 4.
AUB é o conjunto dos elementos que pertencem a A ou B:
Regiões 2, 3 e 4.
Logo, (C\A) ∩ (AUB) é formado apenas pelos elementos que estão na região 4.
(C∩B) é o conjunto dos elementos que estão em C e B ao mesmo tempo:
Regiões 3 e 4.
Logo a afirmação é falsa.
Resposta: Errado.
Veja a resolução no YouTube
Gostou da prova resolvida de raciocínio lógico matemático do concurso para técnico do INSS 2016?
Deixe o seu comentário.

Olá! Sou o Wilson
Fiquei na dúvida da pergunta num 50 do caderno do inn de raciocínio lógico.
Boa tarde Mestre.
Qual o seu posicionamento por gentileza acerca desta interpretação:
“O item não informa como se comportam os conjuntos A e B, ou seja, se são disjuntos ou não,desta forma caberia uma outra interpretação, pois se os conjuntos A e B forem disjuntos teremos a assertiva como verdadeira, isto é
(C\A) ∩ (A U B) = C ∩ B.”
Obrigado por sua atenção.
Referente a questão 50, raciocinei por uma linha na hora da prova, tem algum sentido ou esta totalmente incorreto.
Conforme informado o conjunto C contem os conjuntos A e B, caso o conjunto C não possua mais nenhum elemento além de A e B teremos:
C\A = B e A U B = C
então:
(C\A) n (A U B) = C n B
B n C = C n B
Caros amigos, recebi alguns questionamentos sobre a questão 50. Cabe ou não recurso?
Eu entendo que não é passível de recurso, pois devemos verificar se a igualdade vale para todos os casos. Vimos que quando existe elemento em C que não pertence a AUB, a igualdade não é verdadeira.
No máximo poderíamos alegar que a questão foi mal enunciada, mas o Cespe pensa várias vezes antes de anular uma questão.
Boa sorte a todos!
Professor, discordo de sua colocação. A questão apenas pergunta se a afirmação é correta. Não coloca mais nenhuma circunstância.
Então neste caso coloco como CERTO ou anularia a questão, pois faltam dados.
Ronald, a questão realmente gerou muitas dúvidas. Deve ter muitos recursos, mas mudar para Certo não faz sentido pois existe um caso onde a afirmativa é falsa. No máximo anular a questão.
Boa sorte!