Estudando matemática e raciocínio lógico para o concurso do Departamento Penitenciário Nacional (DEPEN)? Confira aqui a prova resolvida do concurso realizado pelo CESPE em 2013.

Não deixe de ver também as nossas provas resolvidas de outros concursos do CESPE e de outras bancas.

Boa sorte!

 

 

Uma pessoa guardou em seu bolso duas notas de R$ 100, três notas de R$ 50 e quatro notas de R$ 20. Essa pessoa deseja retirar do bolso, de forma aleatória, sem olhar para dentro do bolso, pelo menos uma nota de cada valor. Considerando essa situação, julgue os itens a seguir.

 

Questão 36. Para que ao menos uma nota de cada valor seja retirada do bolso, a pessoa deverá retirar, no máximo, uma quantia equivalente a R$ 410.

Questão anulada.

 

 

Questão 37. Para que ao menos uma nota de cada valor seja retirada do bolso, a pessoa deverá retirar, pelo menos, oito notas.

Resolução:

duas notas de R$ 100

três notas de R$ 50

quatro notas de R$ 20

Como queremos que ele retire pelo menos uma nota de cada, vamos analisar a pior situação, onde ele pega todas as notas de R$ 20, todas as notas de R$ 50 e termina pegando uma de R$ 100. Ou seja, pegando 8 notas, garantimos que ao menos uma nota de cada valor seja retirada.

Resposta: C

 

 

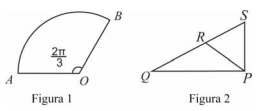
Abaixo, a figura 1 apresenta o arco de circunferência AB correspondente ao ângulo central 2π/3 de uma circunferência de centro O e raio AO = 12 cm e a figura 2 apresenta alguns triângulos. A partir dessas informações e considerando que XY denote a distância entre os pontos X e Y, considere, ainda, as seguintes proposições:

U: o comprimento do arco AB é maior do que OA + OB

V: QR + RP + PS < QP + PS

Com base nas informações e nas figuras acima apresentadas e tomando 3,14 como valor aproximado de π, julgue o item a seguir.

 

Questão 38. A proposição U ⇒ V é falsa

Resolução:

Analisando a tabela verdade condicional, para que a proposição seja falsa, é necessário que U seja verdadeira e V seja falsa.

 

Analisando a proposição U:

Como a circunferência tem raio igual a 12cm, OA + OB = 24cm.

Para calcularmos o tamanho do arco AB, devemos considerar que a fórmula C = 2π.r representa o comprimento de toda a circunferência e que o ângulo em questão é 2π/3:

C = (2π/3).r = (2.3,14/3).12 = 25,12 cm

Logo, a proposição U é verdadeira.

 

Analisando a proposição V:

Utilizando as desigualdades triangulares temos que QP < QR + RP

Somando PS em ambos os lados:

QP + PS < QR + RP + PS

Comparando com a proposição V, temos que ela é falsa.

 

Daí, U ⇒ V é falsa

Resposta: C

 

 

Gostou da prova resolvida do concurso DEPEN 2013?

Deixe o seu comentário.