Confira aqui as mais importantes propriedades dos determinantes, ferramentas poderosas que auxiliam e agilizam a resolução de questões.

Não deixe de ver também nossos conteúdos sobre os outros tópicos da álgebra linear.

Bom estudo!

 

 

PROPRIEDADE 1

Sempre que uma matriz apresentar todos os elementos de uma mesma linha (ou coluna) iguais a zero, o valor do seu determinante também será zero.

 

Exemplo:

 

 

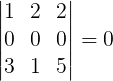
PROPRIEDADE 2

Sempre que uma matriz apresentar duas linhas (ou duas colunas) iguais, o valor do seu determinante será igual a zero.

 

Exemplo:

 

 

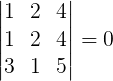
PROPRIEDADE 3

Toda matriz que apresente duas linhas (ou duas colunas) com elementos de valores proporcionais, o valor do determinante será igual a zero.

 

Exemplo:

 

 

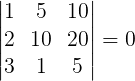
PROPRIEDADE 4

Quando multiplicamos todos os elementos de uma linha (ou coluna) de uma matriz por uma constante k, o determinante da nova matriz passa a ser multiplicado por k.

 

Exemplo:

 

 

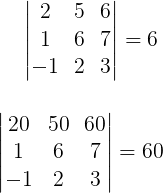
PROPRIEDADE 5

Quando multiplicamos uma matriz quadrada A por um número real k, o novo determinante passa a ser multiplicado por kⁿ, onde n é a ordem da matriz A.

det(k.A) = kⁿ . detA

 

Exemplo:

 

 

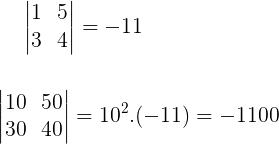
PROPRIEDADE 6

O valor do determinante de uma matriz transposta é igual ao determinante da matriz original.

DetA = det(A^t)

 

 

PROPRIEDADE 7

Quando trocamos duas linhas (ou duas colunas) de posição em uma matriz, o valor do determinante passa a ser o oposto do determinante da matriz original.

 

Exemplo:

 

 

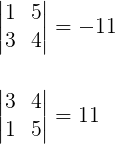
PROPRIEDADE 8

O valor do determinante de uma matriz triangular pode ser calculado apenas multiplicando os elementos da diagonal principal.

 

Exemplo:

 

 

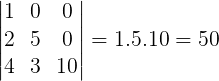
PROPRIEDADE 9

Dadas duas matrizes quadradas de mesma ordem, o determinante do produto é igual ao produto dos determinantes.

det(A.B) = detA . detB

 

 

PROPRIEDADE 10

Quando multiplicamos todos os elementos de uma mesma linha (ou coluna) por um mesmo número e somamos a outra linha (ou coluna), temos uma nova matriz que apresenta o mesmo determinante da anterior.

 

 

PROPRIEDADE 11

O determinante da matriz inversa é o inverso do determinante da matriz original.

 

 

Gostou do nosso conteúdo sobre as propriedades dos determinantes?

Deixe o seu comentário.