Progressão Aritmética

Confira aqui todo o que você precisa saber sobre a Progressão Aritmética, muito conhecida pela abreviação PA Vamos falar sobre a definição, a fórmula do termo geral, e a fórmula da soma dos termos, com muitos exemplos, é claro.

Bom estudo a todos!

Introdução

Observe a sequência de números:

2, 5, 8, 11, 14, 17, 20, 23, 26…

É fácil observar que a sequência tem um padrão, a diferença entre um termo e o seu antecessor é sempre igual a 3.

Toda sequência com essas características é chamada de Progressão Aritmética.

Definição

Progressão Aritmética (PA) é uma sequência de números reais onde a diferença entre um termo e o seu antecessor é sempre a mesma. Essa diferença constante recebe o nome de razão e é representada pela letra r.

Vejamos alguns exemplos de progressões aritméticas para facilitar o nosso entendimento.

Exemplo 1:

1, 2, 3, 4, 5, 6, 7, 8, … (r = 1)

Exemplo 2:

10, 15, 20, 35, 40, … (r = 5)

Exemplo 3:

20, 10, 0, -10, -20, … (r = -10)

Exemplo 4:

0, 1/2, 1, 3/2, 2, 5/2, … (r = 1/2)

Exemplo 5:

6, 6, 6, 6, 6, 6, 6, 6, … (r = 0)

Razão

Analisando os exemplos, podemos classificar as Progressões Aritméticas de acordo com os valores de r:

• Quando r > 0, dizemos que a PA é crescente, como nos exemplos 1, 2 e 4;
• Quando r < 0, dizemos que a PA é decrescente, como no exemplo 3;
• Quando r = 0, dizemos que a PA é constante, como no exemplo 5.

Termo Geral

O fato da progressão aritmética possuir um padrão nos ajuda a saber como ela se comporta. Basta conhecermos a razão e o primeiro termo da PA para conseguirmos obter qualquer outro.

Para isto temos a “fórmula do termo geral da PA”. Veja:

Seja a sequência abaixo uma PA de razão r e primeiro termo a1.

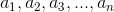
Podemos descobrir o n-ésimo termo dessa sequência através da fórmula:

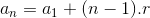
Vejamos alguns exemplos de como podemos utilizar a fórmula do termo geral da PA:

Exemplo 6:

Calcular o 25º termo da sequência (5, 9, 13, 17,…)

Resolução:

O primeiro passo é identificar a razão. Percebe-se que a diferença entre um termo e o seu antecessor é sempre 4, logo r=4.

O primeiro termo da PA é 5 e utilizaremos n=25, pois buscamos o 25º termo.

Vamos utilizar a fórmula do termo geral:

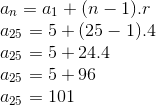
Exemplo 7:

Calcular o 12º termo da sequência (15, 10, 5, 0, -5, -10,…)

Resolução:

A diferença entre um termo e o antecessor é sempre -5, logo r=-5.

O primeiro elemento é o 15 e vamos considerar n=12.

Utilizando a fórmula do termo geral:

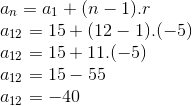
Soma dos termos

Vamos agora aprender a somar os termos de uma Progressão Aritmética finita apenas conhecendo o primeiro e o último e a quantidade de termos.

Veja a fórmula da soma dos termos de uma PA:

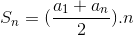
Vejamos alguns exemplos de como podemos utilizar a fórmula.

Exemplo 8:

Calcular o valor de 1+2+3+4+…+100

Resolução:

Analisando a PA, temos que o primeiro termo é 1, o último é 100 e a quantidade também é 100.

Utilizando a fórmula:

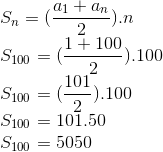
Exemplo 9:

Calcular a soma dos números pares de 2 a 50

Resolução:

Considerando os pares de 2 a 50, temos uma PA de razão 2 com 25 termos, primeiro termo 2 e último termo 50.

Utilizando a fórmula:

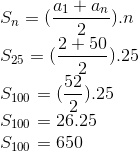
Gostou do nosso conteúdo sobre as Progressões Aritméticas? Ajude a difundir a matemática compartilhando nas redes sociais.