Confira aqui como é feito o cálculo da probabilidade de experimentos binominais.
Pede-se que o aluno já tenha lido os conteúdos iniciais sobre probabilidade e também tenha conhecimentos sobre potenciação.
Bom estudo!
Definição
Experimentos binominais são experimentos onde são possíveis apenas dois resultados. O exemplo mais comum é o lançamento de uma moeda, que pode ter como resultado cara ou coroa. Mas existem outros, como o resultado de um exame, que pode ser positivo ou negativo, o “chute” em uma questão de prova, que pode ter como resultado um acerto ou um erro, dentre outros.
Todo experimento repetido por uma quantidade finita de vezes, em condições idênticas, e cujas repetições são consideradas eventos independentes são chamados de experimentos binominais.
Vamos analisar alguns exemplos para mostrar como é calculada a probabilidade nesses tipos de experimentos.
EXEMPLO 1. Uma moeda é lançada 6 vezes. Qual é a probabilidade de obtermos 4 caras (K) e 2 coroas (C)?
Como vimos, trata-se de um experimento binominal. Vamos calcular em três etapas.
Etapa 1:
O primeiro passo é calcular a probabilidade de obtermos 4 caras e 2 coroas em uma determinada ordem, por exemplo, KKKKCC.
Como os lançamentos são independentes, a chance de acontecer nesta ordem é:
P = P(K ∩ K ∩ K ∩ K ∩ C ∩ C)
P = P(K) . P(K) . P(K) . P(K) . P(C) . P(C)
P = 1/2 . 1/2 . 1/2 . 1/2 . 1/2 . 1/2
P = 1/64
Etapa 2:
Agora que calculamos a probabilidade de acontecer em determinada ordem, vamos analisar todas as ordens possíveis.
Nosso objetivo é analisar a permutação de 6 elementos, com 4 repetições da letra K e 2 repetições da letra C. Podemos fazer um paralelo com o cálculo de anagramas. Temos:
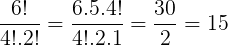
Etapa 3:
Agora que sabemos a probabilidade de ocorrerem 4 caras e 2 coroas em uma determinada ordem, e também de quantas formas isto pode acontecer, a probabilidade pedida é dada por:
15 x 1/64 = 15/64 ≅ 23%
EXEMPLO 2. Um aluno está ficando sem tempo e decide “chutar” as últimas 8 questões de uma prova de múltipla escolha. Sabendo que cada questão possui 5 alternativas, qual a probabilidade do aluno acertar 3 das 8 questões?
Trata-se de um experimento repetido por uma quantidade finita de vezes, em condições idênticas, e cujas repetições são consideradas eventos independentes, ou seja, é um experimento binominal.
Neste caso, a chance do aluno acertar uma questão é de 1/5 e a chance de errar uma questão é de 4/5.
Vamos calcular em três etapas:
Etapa 1:
O primeiro passo é calcular a probabilidade do aluno acertar 3 e errar 5 questões em uma determinada ordem, por exemplo, CCCEEEEE.
Como os lançamentos são independentes, a chance de acontecer nesta ordem é:
P = P(C ∩ C ∩ C ∩ E ∩ E ∩ E ∩ E ∩ E)
P = P(C) . P(C) . P(C) . P(E) . P(E) . P(E) . P(E) . P(E)
P = 1/5 . 1/5 . 1/5 . 4/5 . 4/5 . 4/5 . 4/5 . 4/5
P = 1024/390625
Etapa 2:
Agora que calculamos a probabilidade de acontecer em determinada ordem, vamos analisar todas as ordens possíveis.
Nosso objetivo é analisar a permutação de 8 elementos, com 3 repetições da letra C e 5 repetições da letra E. Podemos fazer um paralelo com o cálculo de anagramas. Temos:
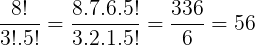
Etapa 3:
Agora que sabemos a probabilidade do aluno acertar 3 e errar 5 questões em determinada ordem, e também de quantas formas isto pode acontecer, a probabilidade pedida é dada por:
56 x 1024/390625 = 57344/390625 ≅ 0,147 = 14,7%
Aprendeu a calcular a probabilidade de experimentos binominais?
Deixe o seu comentário.
