Gostaria de saber mais sobre os Poliedros? Nesta página você verá a definição e alguns exemplos desta figura geométrica.
Não deixe de ler nossos outros conteúdos sobre a geometria espacial.
Bom estudo!
DEFINIÇÃO
Poliedros são sólidos geométricos (três dimensões), cuja superfície é formada por um número finito de superfícies planas (polígonos). Vejamos alguns exemplos:
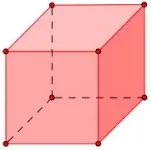
Exemplo 1
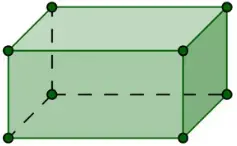
Exemplo 2
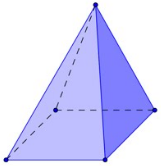
Exemplo 3
ELEMENTOS
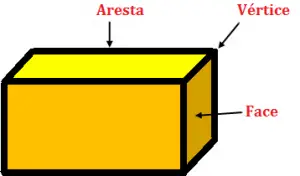
Os elementos principais de um poliedro são as faces, os vértices e as arestas.
- faces – polígonos que limitam o poliedro.
- arestas – são os lados dos polígonos.
- vértices – são os vértices dos polígonos.
Exemplo 4
CLASSIFICAÇÃO DOS POLIEDROS
a) Convexo ou não convexo.
Um poliedro é dito convexo quando qualquer plano que contenha uma face deixa as demais no mesmo semi espaço.
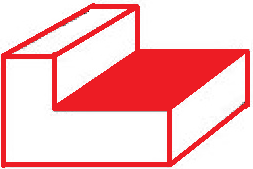
Perceba que isto acontece nos exemplos 1, 2 e 3, onde qualquer plano que contenha uma face deixa das demais no mesmo sem espaço, porém não acontece no exemplo abaixo, onde o plano que contém a face em vermelho separa as demais em dois semi espaços. Veja:
Exemplo 5
b) Regular ou irregular
Um poliedro é regular quando:
– as faces são polígonos regulares e congruentes;
– em todos os seus vértices concorre o mesmo número de arestas.
Observe que o poliedro do exemplo 1, que é regular, enquanto o poliedro do exemplo 2 é irregular.
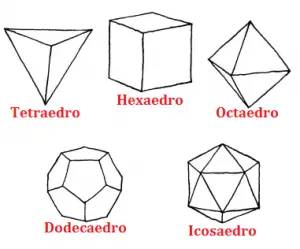
POLIEDROS DE PLATÃO
Todo poliedro convexo e regular recebe uma denominação especial. São os chamados Poliedros de Platão. São eles:
- Tetraedro
- Octaedro
- Icosaedro
- Hexaedro
- Dodecaedro