Você sabe o que é uma função? Veremos aqui a definição e vários exemplos deste importantíssimo conteúdo da matemática.
Bom estudo!
Introdução
O que é uma função? Com certeza você já se fez essa pergunta não é mesmo? As funções possuem diversas aplicações no mundo atual, onde relacionam grandezas, valores, índices, dentre outros.
Vamos analisar dois exemplos:
Exemplo 1. Imagine um carro que mantém uma velocidade constante de 60 km/h. Isto significa que a cada hora que passa ele percorre 60 km. Veja:
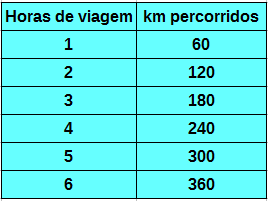
Repare que existem duas grandezas, a distância (km) e o tempo (horas), e que a quantidade de km percorridos depende da quantidade de horas de viagens. Dizemos neste caso que a distância percorrida está em função do tempo.
Neste exemplo podemos achar uma fórmula que estabeleça e relação de interdependência entre a distância (d) e o tempo (t):
d = 60.t
Exemplo 2. Uma fábrica de água de coco compra o fruto em uma fazenda próxima, onde paga R$ 0,20 por coco. Isso significa que o valor de cada compra efetuada depende da quantidade de cocos comprados. Veja:
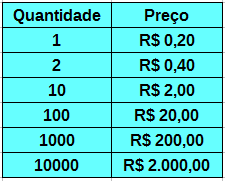
Repare que estão sendo medidas duas grandezas, a quantidade e o preço (R$), e que o preço pago depende da quantidade de cocos comprados. Dizemos neste caso que o preço (p) está em função da quantidade (q) de cocos:
p = 0,20.q
Definição
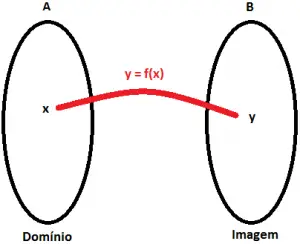
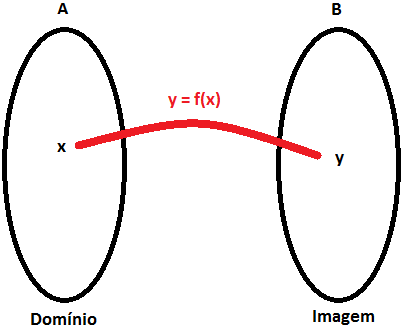
Sejam A e B dois conjuntos não vazios, e f a relação ou regra que associa para cada elemento x de A, um e apenas um elemento y de B. Dizemos neste caso que f é uma função de A em B, e é representada da seguinte forma:
f: A → B
y = f(x)
Exemplo 3:
f: N → N
y = 2x
Nota-se neste caso que a função f relaciona o conjunto dos números naturais, onde leva um número natural ao seu dobro.
O conjunto onde estão todos os valores possíveis de x é chamado de domínio da função e normalmente é representado por D ou Dom. Dizemos ainda que x é a variável independente.
O conjunto onde estão os valores de y que possuem um correspondente em x é chamado de imagem da função e normalmente é representado por I, Im ou f(x). Dizemos que y é a variável dependente, pois como vimos, depende da variável x.
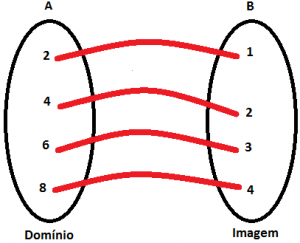
Exemplo 4:
Sejam os conjuntos de números naturais A = {2, 4, 6, 8} e B = 1, 2, 3, 4}, onde f é uma função que associa a cada elemento de A, um elemento de B que corresponde a sua metade. Temos:
f: A → B
y = x/2
Gostou da nossa publicação sobre função? Compartilhe o nosso conteúdo nas redes sociais e deixe também o seu comentário no final da página. Bons estudos e volte sempre!
Entendi a explicação…é muito bom estudar matemática.