Você sabe o que são os logaritmos? Veremos aqui a definição, alguns exemplos e as propriedades, sendo imprescindível que o aluno tenha conhecimento prévio sobre potenciação.
Bom estudo!
Definição
Dados dois números (reais e positivos) ‘a‘ e ‘b‘, com a≠1, chamamos de logaritmo de ‘b‘ na base ‘a‘, o expoente ‘x‘ tal que ‘a‘ elevado a ‘x‘ seja igual a ‘b‘.
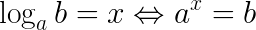
No logaritmo temos:
a = base do logaritmo
b = logaritmando
x = valor do logaritmo
Exemplos
Vejamos alguns exemplos para facilitar nosso entendimento sobre a definição:
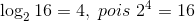
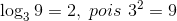
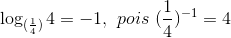
Logaritmos de base 10
Você certamente já deve ter visto em algum livro ou site um logaritmo sem valor explícito na base, como por exemplo log 3. Sempre que isto ocorrer devemos considerar que a base é igual a 10. Veja:
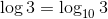
Os logaritmos de base 10 são muito úteis na resolução de problemas que envolvem matemática financeira, principalmente para o cálculo de taxas de juros.
Consequências da definição
Decorrem da definição de logaritmo as seguintes propriedades:
- O logaritmo de 1 é sempre 0 (zero), não importa o valor da base.
Isso ocorre porque todo número elevado a zero é igual a 1.
- Quando o logaritmando é igual a base o logaritmo é sempre igual a 1.
Isso ocorre porque todo número elevado a 1 é igual a ele mesmo.
Propriedades
Vamos agora estudar três propriedades importantíssimas para a resolução de questões envolvendo logaritmos. Para facilitar, vamos utilizar a base 10, mas elas valem para qualquer base.
Propriedade 1: Transformando multiplicação em adição.
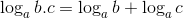
O logaritmo de um produto de dois ou mais números reais e positivos é igual à soma dos logaritmos desses números reais.
Exemplos:
log (3.5) = log 3 + log 5
log 21 = log (3.7) = log 3 + log 7
log 30 = log (2.3.5) = log 2 + log 3 + log 5
Propriedade 2: Transformando divisão em subtração.
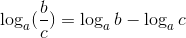
O logaritmo de um quociente de dois números reais e positivos é igual à diferença entre os logaritmos desses números reais.
Exemplos:
log (7/5) = log 7 – log 5
log (1/2) = log 1 – log 2
Propriedade 3: Logaritmo da potência
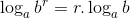
O logaritmo de uma potência de base real e positiva é igual ao produto do expoente pelo logaritmo da base da potência.
Exemplos:
log 4² = 2.log 4
log 2³ = 3.log 2
Mudança de base
Em muitas situações um logaritmo está em uma certa base, porém seria mais útil se estivesse em outra. Vamos aprender como podemos alterar as bases visando facilitar a resolução dos exercícios.
Por exemplo, as propriedades dos logaritmos só podem ser aplicadas quando possuem a mesma base. Essa mudança também é muito útil para mudarmos para a base 10, que é a mais utilizada.
Veja como funciona:
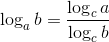
Exemplos:
- Quando queremos utilizar a base 5:
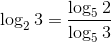
- Quando queremos utilizar a base 10:
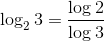
Aprendeu ao importante sobre os logaritmos? Deixe seu comentário e compartilhe nas redes sociais.
Até a próxima!
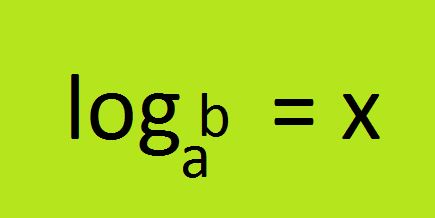
Muito bom. Aprendi muito e revisei algumas propriedades !