Veja nesta página uma seleção especial de exercícios resolvidos sobre função afim, também chamada de função do primeiro grau.
Lembrando que todos os exercícios foram retirados de questões de concursos realizados pelo Brasil nos últimos anos.
Bons estudos e boa sorte!
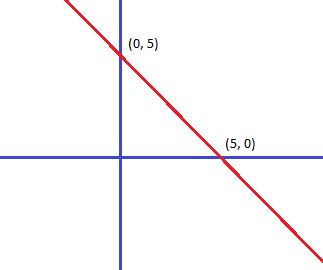
Questão 1 (PM ES – Exatus). Em linguagem matemática, sempre que relacionamentos duas grandezas variáveis estamos empregando o conceito de função. A função y = -x + 5 é chamada função polinomial do 1º grau. Represente o seu gráfico.
Resolução
O gráfico de uma função do primeiro grau, também chamada de função afim, tem o formato de uma reta.
Considerando a equação reduzida de uma reta (y = a.x + b), temos que:
a = -1
b = 5
O número a = -1 é chamado de coeficiente angular, e indica se a reta é crescente ou decrescente. Como a<0, a reta será decrescente.
O número b = 5 é chamado de coeficiente linear, e indica o ponto do eixo y que é cortado pela reta, ou seja, (0, 5).
Considerando y = 0, também podemos concluir que a reta corta o eixo x no ponto (5, 0).
Com essas informações, é possível desenhar o gráfico da função afim:
Questão 2 (PRF – Cespe). Considere que, em 2009, tenha sido construído um modelo linear para a previsão de valores futuros do número de acidentes ocorridos nas estradas brasileiras. Nesse sentido, suponha que o número de acidentes no ano t seja representado pela função F(t) = At + B, tal que F(2007) = 129.000 e F(2009) = 159.000. Com base nessas informações e no gráfico apresentado, julgue os itens a e b.
a) É verdade que “O valor da constante A em F(t) é superior a 14.500”?
Resolução:
Basta observar que temos uma função afim, onde sabemos dois pontos, assim fica fácil descobrir os valores de A e B.
1) 129000 = 2007A + B
2) 159000 = 2009A + B
1) 129000 – 2007A = B
2) 159000 – 2009A = B
Daí,
129000 – 2007A = 159000 – 2009A
2009A – 2007A = 159000 – 129000
2A = 30000
A = 30000/2 = 15000
Resposta: CERTO
b) É verdade que “A diferença entre a previsão para o número de acidentes em 2011 feita pelo referido modelo linear e o número de acidentes ocorridos em 2011 dado no gráfico é superior a 8.000”?
Resolução:
Como já sabemos o valor de A, vamos agora descobrir o valor de B:
F(2009) = 159000
159000 = 2009A + B
159000 = 2009.15000 + B
B = 159000 – 30135000
B = – 29976000
Temos então que nossa função é:
F(t) = 15000t – 29976000
F(2011) = 15000.2011 – 29976000
F(2011) = 189000 e em 2011 tiveram 189000 acidentes
Resposta: ERRADO
Questão 3 (PM SC – Cesiep). Duas empresas A e B têm ônibus com 50 assentos. Em uma excursão para Balneário Camboriú, as duas empresas adotam os seguintes critérios de pagamento:
A empresa A cobra $25,00 por passageiro mais uma taxa fixa de $400,00.
A empresa B cobra $29,00 por passageiro mais uma taxa fixa de $250,00.
Pergunta-se: Qual é o número mínimo de excursionistas para que o contrato com a empresa A fique mais barato do que o contrato da empresa B?
a) 37
b) 38
c) 35
d) 40
Resolução:
Note que em ambas empresas, é cobrado um valor fixo mais uma quantidade por passageiro.
Sendo x a quantidade de passageiros:
A função que representa o valor cobrado pela empresa A em função da quantidade de passageiros é:
f(x) = 25x + 400
A função que representa o valor cobrado pela empresa B em função da quantidade de passageiros é:
f(x) = 29x + 250
Para que a empresa A fique mais barata que a empresa B devemos ter:
29x + 250 > 25x + 400
29x – 25x > 400 – 250
4x > 150
x > 150/4
x > 37,5
Logo, devemos ter pelo menos 38 excursionistas.
Resposta: B
Questão 4 (PM PE – UPENET). Em certa cidade, a bandeirada comum numa corrida de táxi custa R$ 4,32. Na bandeira 1, o cliente paga R$ 2,10 por quilômetro rodado, e na bandeira 2, ele paga R$ 2,54. Se Carlos pagou R$ 65,28 por uma corrida na bandeira 2, qual foi a quilometragem de sua corrida?
A) 20 km
B) 26 km
C) 24 km
D) 28 km
E) 30 km
Resolução
A função afim que representa o custo em relação a quilometragem rodada na bandeira 2 é:
c(x) = 4,32 + 2,54.x
Como ele pagou 65,28:
65,28 = 4,32 + 2,54.x
65,28 – 4,32 = 2,54.x
2,54x = 60,96
x = 60,96/2,54
x = 24
Resposta: C
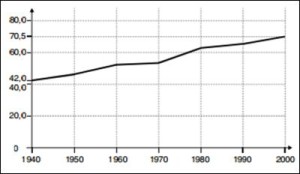
Questão 5 (INSS 2008 – Cespe). Um dos indicadores de saúde comumente utilizados no Brasil é a esperança de vida ao nascer, que corresponde ao número de anos que um indivíduo vai viver, considerando-se a duração média da vida dos membros da população. O valor desse índice tem sofrido modificações substanciais no decorrer do tempo, à medida que as condições sociais melhoram e as conquistas da ciência e da tecnologia são colocadas a serviço do homem.
A julgar por estudos procedidos em achados fósseis e em sítios arqueológicos, a esperança de vida do homem pré-histórico ao nascer seria extremamente baixa, em torno de 18 anos; na Grécia e na Roma antigas, estaria entre 20 e 30 anos, pouco tendo se modificado na Idade Média e na Renascença. Mais recentemente, têm sido registrados valores progressivamente mais elevados para a esperança de vida ao nascer. Essa situação está ilustrada no gráfico abaixo, que mostra a evolução da esperança de vida do brasileiro ao nascer, de 1940 a 2000.
Com base nas informações do texto e considerando os temas a que ele se reporta, julgue o item seguinte.
“Se E representa a esperança de vida do brasileiro ao nascer e x representa o tempo, em anos, transcorrido desde 1940, infere-se das informações apresentadas que, para 0 ≤ x ≤ 60, E(x) = 42x + 70,5.”
Resolução:
Observe que temos 60 anos entre 1940 e 2000, assim, x=0 representa o ano 1940 e x=60 representa o ano 2000.
Dada a função E(x) = 42x + 70,5, vamos considerar x=0.
E(0) = 42.0 + 70,5 = 70,5
Veja que x=0 representa o ano de 1940, logo, E(0) deveria ser 42 e não 70,5.
Resposta: Errado
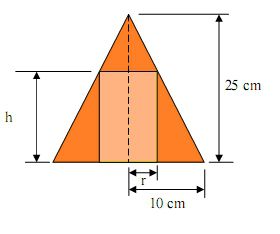
Questão 6 (PRF 2008 – Cespe). Considere que um cilindro circular reto seja inscrito em um cone circular reto de raio da base igual a 10 centímetros e a altura igual a 25 centímetros, de forma que a base do cilindro esteja no mesmo plano da base do cone. Em face dessas informações e, considerando, ainda, que h e r correspondam à altura e ao raio da base do cilindro, respectivamente, assinale a opção correta.
a) A função afim que descreve h como função de r é crescente.
b) O volume do cilindro como uma função de r é uma função quadrática.
c) Se A(r) é a área lateral do cilindro em função de r, então A(r) = 50 π r (1 – r/10)
d) É possível encontrar um cilindro de raio da base igual a 2 centímetros e altura igual a 19 centímetros que esteja inscrito no referido cone.
e) O cilindro de maior área lateral que pode ser inscrito no referido cone tem raio da base superior a 6 centímetros.
Resolução:
Veja na figura que o cilindro está dentro do cone.
Vamos agora analisar cada uma das alternativas.
a) A função afim que descreve h como função de r é crescente.
Basta verificar que a medida que r aumenta, h diminui, ou seja, a função é decrescente.
Para encontrar a equação de h, vamos usar o método dos triângulos proporcionais. Se o triângulo maior, ABC, e o triângulo menor CDE. Veja:
(o fato de -25/10 ser negativo nos prova que a função afim é decrescente)
(o fato de -25/10 ser negativo nos prova que a função afim é decrescente)
b) O volume do cilindro como uma função de r é uma função quadrática.
V = π.r².h = π.r².(25 – 25r/10) = 25π.r² – 25π.r³/10
Veja que a função é cúbica e não quadrática.
c) Se A(r) é a área lateral do cilindro em função de r, então A(r) = 50 r.
A(r) = base.altura = 2π.r.h = 2π.r.(25 – 25r/10) = 50π.r (1 – r/10)
d) É possível encontrar um cilindro de raio da base igual a 2 centímetros e altura igual a 19 centímetros que esteja inscrito no referido cone.
h = 25 – 25r/10 = 25 – 25.2/10 = 25 – 5 = 20
e) O cilindro de maior área lateral que pode ser inscrito no referido cone tem raio da base superior a 6 centímetros.
A(r) = 50π.r (1 – r/10) = 50π.r – 5π.r². (função quadrática decrescente, o ponto máximo de r é o vértice)
xv = -b/2a – -50π/2(-5π) = 5
Resposta: C
Questão 7 (Caixa 2006 – Cespe). A CAIXA criou as Cestas de Serviços com o compromisso de valorizar o relacionamento com seus clientes e oferecer cada vez mais vantagens.
Você paga apenas uma tarifa mensal e tem acesso aos produtos e serviços bancários que mais se adequarem ao seu relacionamento com a CAIXA.
Alguns dos itens disponíveis têm seu uso limitado. Caso você exceda as quantidades especificadas ou utilize um item não incluso na sua cesta, será cobrado o valor daquele 10 produto ou serviço discriminado na Tabela de Tarifas vigente.
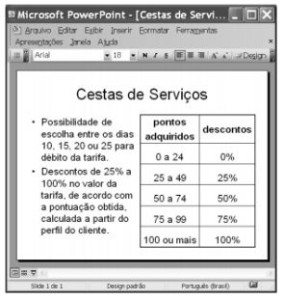
A janela do PowerPoint 2003 a seguir apresenta, no slide em edição, outras informações acerca das Cestas de Serviços da CAIXA.
Com base nas informações do texto e sabendo que, a cada R$ 100,00 de saldo médio no trimestre em aplicação na poupança, o cliente acumula 1 ponto para o cálculo do desconto na tarifa mensal de serviços, julgue os seguintes itens.
a) Suponha que se deseje representar os percentuais de descontos concedidos em função dos pontos adquiridos — que são elementos do conjunto dos números naturais N = {0, 1, 2, …} —, de acordo com o que está estabelecido na tabela apresentada na janela do PowerPoint. Para isso, se, para cada n Є N, for representado por d(n) o desconto correspondente, então a função d pode ser corretamente descrita pela seguinte expressão:
CORRETO
Perceba que a função d(n) está de acordo com os intervalos de n representados na figura.
b) De acordo com as informações apresentadas, há possibilidade de o cliente obter isenção total da tarifa mensal de serviços.
CORRETO
Observar a última linha da tabela.
Questão 8 (Petrobrás 2010). A função g(x) = 84.x representa o gasto médio, em reais, com a compra de água mineral de uma família de 4 pessoas em x meses. Essa família pretende deixar de comprar água mineral e instalar em sua residência um purificador de água que custa R$ 299,90. Com o dinheiro economizado ao deixar de comprar água mineral, o tempo para recuperar o valor investido na compra do purificador ficará entre
(A) dois e três meses.
(B) três e quatro meses.
(C) quatro e cinco meses.
(D) cinco e seis meses.
(E) seis e sete meses.
Resolução:
Como a função afim g(x) representa o gasto médio e queremos saber quando o investimento de 299,90 será recuperado, basta igualarmos:
84.x = 299,90
x = 299,90 / 84
x = 3,57
Logo, entre 3 e 4 meses.
Resposta: B
Questão 9 (PM ES – AOCP). O esboço de gráfico a seguir mostra a relação linear entre o custo y (em reais) da produção de x coletes de segurança:
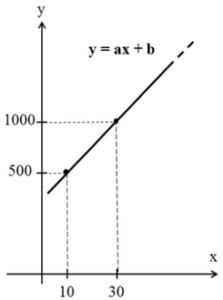
Se forem gastos R$ 2.000,00 na produção de um lote de coletes, então, nesse lote, foram produzidos
A) 70 coletes.
B) 90 coletes.
C) 50 coletes.
D) 80 coletes.
E) 60 coletes.
Resolução
A questão pode ser facilmente resolvida apenas observando no gráfico que a cada aumento de 20 coletes, o custo de produção cresce em 500.
Considerando o ponto (30, 1000), podemos concluir que quando o custo aumenta para 2000, a quantidade de coletes produzida é de 70.
A resolução mais formal seria calcular a equação da reta, considerando que temos dois pontos (10, 500) e (30, 1000).
Para tanto, basta resolvermos o sistema de equações do primeiro grau:
500 = 10a + b
1000 = 30a + b
Resolvendo o sistema, temos:
a = 25
b = 250
A equação reduzida da reta será:
y = 25x + 250
Considerando y = 2000:
2000 = 25x + 250
25x = 2000 – 250
25x = 1750
x = 1750/25
x = 70
Resposta: A
Gostou dos nossos exercícios resolvidos sobre função afim (função do primeiro grau)?
Deixe o seu comentário.

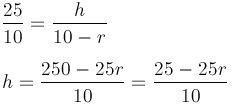
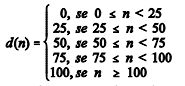
sou priscila es muito inteligente em to muito preocupada sexta faco esta prova de matematica aplicada….estou bem preocupda……
Olá Priscila,
Não tem segredo, é só estudar bastante.
Boa sorte!
Professor como que chegou aos numeros 2, ns resolucão da questão 4?
Shay,
A questão estava incompleta e foi substituída.
*é muito dificil mesmo*
As questões me ajudaram muito!