Hoje vamos aprender um pouco sobre a função afim, também chamada de função do primeiro grau, uma importante ferramenta matemática para analisarmos grandezas proporcionais.
Nesta página abordaremos a definição e a construção do gráfico no plano cartesiano, sempre utilizando exemplos para facilitar a compreensão.
Bons estudos!
Introdução
A locadora de veículos Carro Bom trabalha da seguinte forma: O cliente paga uma taxa de R$ 50,00 ao ceder o veículo e R$ 1,50 a cada km rodado. Como o cliente pode calcular o valor a ser pago?
Veja que pelo contrato assinado com a locadora existe um custo fixo de R$ 50,00, e um custo variável, de acordo com a quantidade de km rodados pelo cliente.

O custo total pode ser calculado da seguinte forma:
Custo Total = Custo Fixo + Custo Variável
Considerando que o cliente roda uma quantidade x de km, e que o custo total C está em função de x, a lei matemática que representa essa dependência é:
C(x) = 1,50.x + 50
Veja que C(x) é o custo total em função da quantidade x de km rodados.
A função C(x) é um exemplo da função afim ou função do primeiro grau.
Definição
Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= a.x + b para todo x ∈ R, onde a ≠ 0.
Voltando ao exemplo anterior:
C(x) = 1,50.x + 50
Temos:
a = 1,50
b = 50
Significado dos Coeficientes
Na função f(x)= a.x + b, o número a é chamado de coeficiente de x, enquanto o número b é chamado de termo constante.
Veremos mais a frente que os coeficientes a e b nos ajudam a identificar o gráfico da função.
Exemplos de funções afim e seus coeficientes:
a) f(x) = 2x + 3, onde a=2 e b=3
b) f(x) = -3x + 10, onde a=-3 e b=10
c) f(x) = x + 13, onde a=1 e b=13
Gráfico
O gráfico de uma função afim é uma reta não perpendicular ao eixo x. Veja agora a importância dos coeficientes a e b na identificação do gráfico desse tipo de função.
- Para que serve o coeficiente a?
O coeficiente a, chamado de coeficiente angular da reta e recebe esse nome justamente por determinar o ângulo de inclinação da reta em relação ao eixo Ox. Isto significa que quanto maior o valor de a, maior a inclinação da reta.
O coeficiente angular também determina se a reta é crescente ou decrescente. Veja:
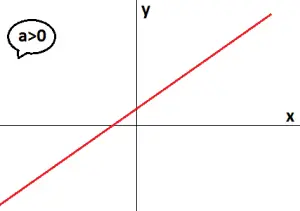
Se a>0, a função afim é crescente.
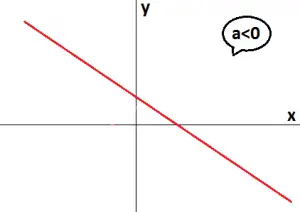
Se a<0, a função afim é decrescente.
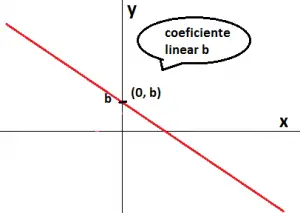
- Para que serve o coeficiente b?
O coeficiente b, também chamado de coeficiente linear da reta, determina o local exato onde a reta corta o eixo Oy. Veja:
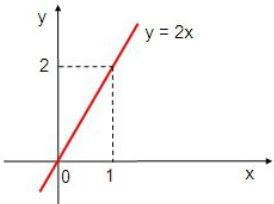
Exemplo 1. f(x) = 2x
O primeiro passo é identificar os coeficientes angular e linear. Temos que:
a = 2
b = 0
Como a = 2, a reta é crescente.
Como b = 0, a reta passa pela origem.
Veja como fica o gráfico de f(x):
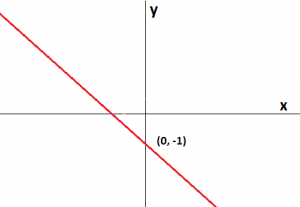
Exemplo 2. f(x) = – x – 1
O primeiro passo é identificar os coeficientes angular e linear. Temos que:
a = -1
b = -1
Como a = -1, a reta é decrescente.
Como b = -1, a reta passa pelo ponto (0,-1).
Veja como fica o gráfico de f(x):
Aprendeu mais sobre a função afim? O conteúdo foi útil? Compartilhe nas redes sociais e deixe seu comentário.
ola eu sou pedro, gostei do site ele muito eficiente pois meu amigo burrrro matheus soares está aprendendo muito com vc então muito obrigado beijo na bunda até segunda!!!! +_+ *_* :::::::::::::