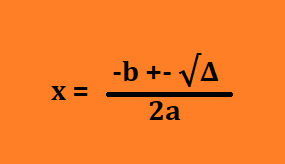Estudando matemática para concursos? Confira aqui qual é a expressão conhecida como fórmula de Bhaskara.
Não deixe de ver também as nossas publicações sobre equações do segundo grau.
Bom estudo!
A fórmula de Bhaskara é utilizada para calcular as raízes de equações do segundo grau.
Ela deve ser aplicada em equações no formato abaixo:
ax² + bx + c = 0
Onde:
x é a incógnita
a, b, c são coeficientes
A fórmula de Bhaskara é dada pela seguinte expressão:
![]()
Como resolver equações do segundo grau com a fórmula de Bhaskara
- Passo 1. Calcular o valor do discriminante
O discriminante é a expressão que consta dentro da raiz quadrada e é representado pela letra grega Delta.
∆ = b² – 4ac
Essa expressão é destacada na fórmula de Bhaskara pelo fato de determinar quantas raízes a equação do segundo grau possui. Veja:
∆ > 0, a equação possui duas raízes reais;
∆ = 0, a equação possui uma raiz real;
∆ < 0, a equação não possui raízes reais.
- Passo 2. Calcular as raízes reais
Caso ∆ não seja negativo, devemos prosseguir com o cálculo das raízes reais utilizando a fórmula de Bhaskara.
Como a fórmula possui um sinal ±, cada uma das raízes é representada por:
![]()
![]()
Exemplo. Calcular as raízes da equação x² – 7x + 12 = 0.
Temos os seguintes coeficientes:
a = 1
b = -7
c = 12
Calculando o valor de delta:
∆ = b² – 4ac
∆ = (-7)² – 4.1.12
∆ = 49 – 48
∆ = 1
Como ∆ > 0, podemos concluir que a equação proposta possui duas raízes reais. Vamos calculá-las?
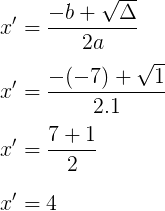
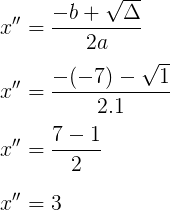
Conclusão: O conjunto solução da equação é S = {3, 4}.
Aprendeu a utilizar a fórmula de Bhaskara?
Deixe o seu comentário.