Confira aqui exercícios resolvidos sobre o trapézio, onde estudaremos a área, o perímetro e os ângulos desta figura plana.
Vale salientar que todos os exercícios foram retirados de provas de concursos públicos das mais variadas bancas.
Bom estudo!
Questão 1 (PC MG 2008 – Acadepol). As medidas da base maior e da altura de um trapézio são, respectivamente, o quíntuplo e o dobro da medida de sua base menor. Se a área desse trapézio é 54 cm², a medida de sua base menor, em cm, é
A) 3
B) 4
C) 6
D) 15
Resolução:
Se x a medida da base menor, então:
base maior = 5x
altura = 2x
Pela fórmula da área de um trapézio:
área = (base maior + base menor).altura/2
54 = (5x + x).2x/2
54 = 6x.2x/2
54 = 6x²
x² = 54/6
x² = 9
x = 3 cm
Resposta: A
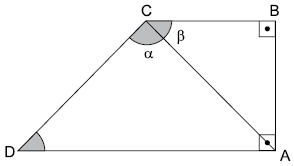
Questão 2 (TJ SP – Vunesp 2015). Na figura, o trapézio retângulo ABCD é dividido por uma de suas diagonais em dois triângulos retângulos isósceles, de lados ![]()
Desse modo, é correto afirmar que a soma das medidas dos ângulos a e b é igual a:
(A) 130º.
(B) 110º.
(C) 115º.
(D) 125º.
(E) 135º.
Resolução
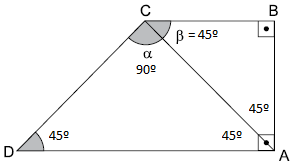
Como AC divide o trapézio retângulo em dois triângulos isósceles, os ângulos do trapézio são:
De onde concluímos que a + b = 90 + 45 = 135º
Resposta: E
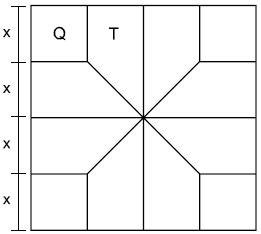
Questão 3 (TJ SP – Vunesp 2014). Para efeito decorativo, um arquiteto dividiu o piso de um salão quadrado em 8 regiões com o formato de trapézios retângulos congruentes (T), e 4 regiões quadradas congruentes (Q), conforme mostra a figura:
Se a área de cada região com a forma de trapézio retângulo é igual a 24 m², então a área total desse piso é, em m², igual a
(A) 225.
(B) 196.
(C) 324.
(D) 400.
(E) 256.
Resolução
A informação de que os trapézios e os quadrados são congruentes é muito importante. Dela tiramos que que a região pode ser dividida em 16 quadrados Q, todos de área x².
Sabemos que a área de cada trapézio é 24m². Também não é difícil verificar, observando as congruências, que a área de cada trapézio é 3/2 da área de cada quadrado. Temos então que a área de cada quadrado é 24.(2/3) = 16m².
Como são 16 quadrados, a área total é:
16.16 = 256m²
Resposta: E
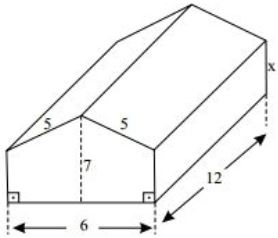
Questão 4 (Sejus ES 2013). Uma tenda de lona foi montada no pátio da penitenciária, com suas medidas em metros e a forma de um prisma reto indicadas na figura. A área total da lona usada na montagem foi 252 m², correspondendo à frente, ao fundo, às laterais e à cobertura.
A altura lateral (x) dessa tenda mede
 (A) 3,0 m.
(A) 3,0 m.
(B) 3,2 m.
(C) 3,5 m.
(D) 2,0 m.
(E) 4,0 m.
Resolução
Área das duas laterais: 2.12x = 24x
Área do teto: 2.5.12 = 120
Área frente/atrás (4 trapézios) = 4(x+7)3/2 = 6x + 42
Daí,
24x + 120 + 6x + 42 = 252
30x = 252 – 120 – 42
30x = 90
x = 90/30 = 3
Resposta: A