Confira nesta página alguns exercícios resolvidos sobre a função logarítmica. É fundamental que você tenha lido nosso material sobre esse tipo de função e que também tenha um bom conhecimento sobre a definição de funções e logaritmos.
Lembrando que os exercícios foram retirados de questões dos últimos concursos realizados pelo país.
Bom estudo!
Questão 1 (PM PR 2010). Considere as afirmativas:
I- A função logarítmica na base 2, para x>0 é sempre positiva.
II- A função logarítmica natural f(x) = ln(x), para x>0 é sempre crescente.
III- A função cosseno f(x) = cos(x), para x>0, é sempre positiva.
IV- A função tangente, f(x) = tg(x), para 0 < x < π/2, é sempre crescente.
Quais as únicas alternativas corretas?
a) I e II
b) II e IV
c) III e IV
d) I, II e III
e) I, III e IV
Resolução
I) Falsa. Será negativa quando 0 < x < 1.
II) Verdadeira. O número de Euler é aproximadamente 2,718 > 1, fazendo com que a função seja crescente para x > 0.
III) Falsa. A função Cosseno varia entre 1 e -1
IV) Verdadeira. A função tangente é sempre crescente para x > 0.
Resposta: B
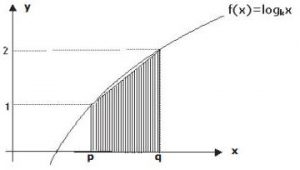
Questão 2 (Espcex 2011). Na figura abaixo, dois vértices do trapézio sombreado estão no eixo x e os outros dois vértices estão sobre o gráfico da função real f(x)=log(k) x, com k>0 e k≠1. Sabe−se que o trapézio sombreado tem 30 unidades de área; assim, o valor de k+p−q é
 a) −20
a) −20
b) −15
c) 10
d) 15
e) 20
Resolução
Analisando a figura, vamos utilizar a fórmula da área do trapézio, onde:
lado maior = 2
lado menor = 1
altura = q – p
área = 30
(q – p)(1 + 2)/2 = 30
(q – p).3/2 = 30
(q – p).1,5 = 30
q – p = 20
Agora vamos analisar os dois pontos que sabemos do gráfico, utilizando a definição de logaritmos. Temos:
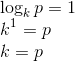
![]()
Substituindo na equação anterior:
q – p = 20
k² – k – 20 = 0
Resolvendo a equação do segundo grau através do método da soma e do produto:
Soma = -b/a = 1
Produto = c/a = -20
Os dois números cuja soma é 1 e o produto é -20 são -4 e 5.
Como k é a base do logaritmo, não pode assumir valor negativo, logo k = 5.
Daí, p = 5 e q = 25
Finalizando,
k + p − q = 5 + 5 – 25 = -15
Resposta: B