Estudando matemática para concursos? Confira nesta página tudo sobre a equação reduzida da circunferência.
Não deixe de ver também nossos conteúdos sobre os outros tópicos da geometria analítica.
Bom estudo!
Uma circunferência de centro C(xc, yc) e raio r é o conjunto de todos os pontos do plano que estão a uma distância r do centro. Veja:
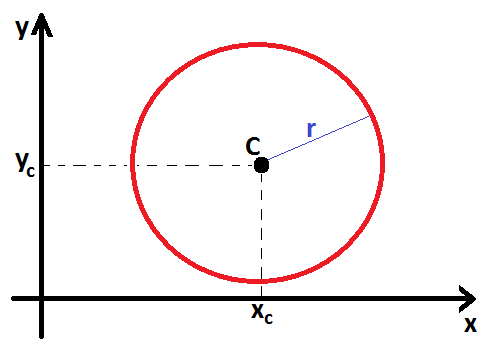
Sendo P(x, y) um ponto qualquer da circunferência, vamos aplicar o Teorema de Pitágoras no triângulo ACP.
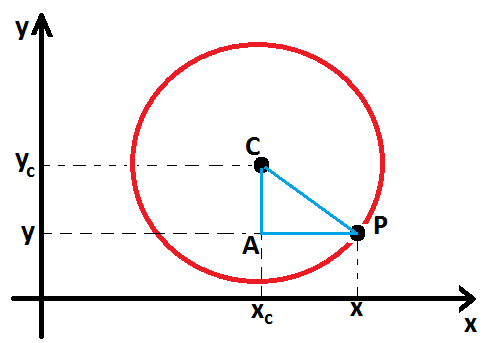
Veja que:
CP = r (raio da circunferência)
AC = yc – y
AP = x – xc
Pelo Teorema de Pitágoras:
CP² = AC² + AP²
r² = (yc – y)² + (x – xc)²
Daí, a equação (x – xc)² + (y – yc)² = r² é chamada de equação reduzida da circunferência, onde:
- xc e yc são as coordenadas do centro C da circunferência;
- r é o raio da circunferência;
- x e y são as coordenadas de um ponto P qualquer da circunferência.
Exemplo 1. A equação abaixo é a equação reduzida da circunferência de centro C(2, 3) e raio 5.
(x – 2)² + (y – 3)² = 25
Exemplo 2. A equação abaixo é a equação reduzida da circunferência de centro C(1, -3) e raio 2.
(x – 1)² + (y + 3)² = 4
Exemplo 3. A equação abaixo é a equação reduzida da circunferência de centro C(0, -10) e raio 1.
x² + (y + 10)² = 1
Gostou do nosso conteúdo sobre a equação reduzida da circunferência?
Curta e compartilhe nas redes sociais.
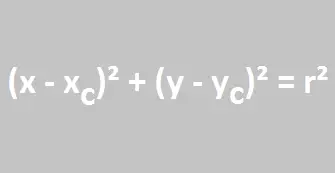
gostei muito , ajudou na compreensão e ja estou divulgando para todos meus amigos