Dando continuidade ao estudo da geometria analítica, nesta página aprenderemos sobre a equação geral da reta.
Não deixe de ver também nossos outros tópicos sobre a geometria analítica e sobre equações.
Bom estudo!
Chamamos de equação geral da reta a toda equação do tipo a.x + b.y + c = 0, onde x e y representam as coordenadas dos pontos pertencentes à reta, e a, b e c são constantes reais, onde a e b são diferentes de zero.
![]()
Exemplo 1
2x + 3y + 1 = 0
a = 2
b = 3
c = 1
Exemplo 2
-x + y/2 = 0
a = -1
b = 1/2
c = 0
COMO DETERMINAR A EQUAÇÃO GERAL DA RETA
Dados dois pontos A(xA, yA) e B(xB, yB), a equação geral da reta que passa por esses pontos pode ser determinada desenvolvendo a seguinte expressão:
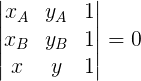
Repare que estamos utilizando a condição de alinhamento de três pontos, onde consideramos (x, y) um ponto qualquer da reta.
Exemplo 3. Determinar a equação geral da reta que passa pelos pontos A(1, 2) e B(5,5).
Temos:
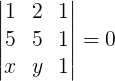
Desenvolvendo o determinante através da regra de Sarrus:
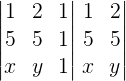
x.5.1 + y.1.1 + 1.5.2 – 1.5.1 – 2.1.x – 1.5.y = 0
5x + y + 10 – 5 – 2x – 5y = 0
3x – 4y + 5 = 0
A equação geral da reta será:
3x – 4y + 5 = 0
Onde:
a = 3
b = -4
c = 5
Exemplo 4. Determinar a equação geral da reta que passa pelos pontos A(0, 2) e B(-1, 4).
Temos:
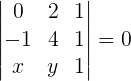
Desenvolvendo o determinante através da regra de Sarrus:
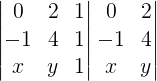
x.4.1 + y.1.0 + 1.(-1).2 – 0.4.1 – 2.1.x – 1.(-1).y = 0
4x + 0 – 2 – 0 – 2x + y = 0
2x + y – 2 = 0
A equação geral da reta será:
2x + y – 2 = 0
Onde:
a = 2
b = 1
c = -2
INFORMAÇÕES FORNECIDAS PELOS COEFICIENTES
O fato de um dos coeficientes a, b ou c da equação geral ax + by + c = 0 ser nulo é bastante relevante no posicionamento da reta. Veja:
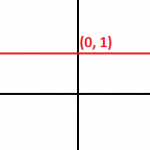
a = 0 ⇒ a reta é horizontal
Exemplo 5
y – 1 = 0
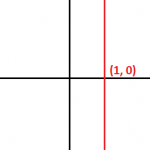
b = 0 ⇒ a reta é vertical
Exemplo 6
x – 1 = 0
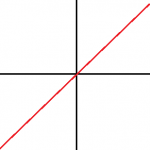
c = 0 ⇒ a reta passa pela origem
Exemplo 7
x + y = 0
Gostou do nosso conteúdo sobre a equação geral da reta?
Deixe o seu comentário e ajude a melhorar este site.
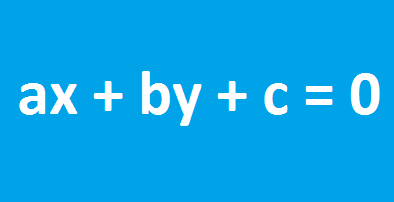
Acho que o cálculo do determinante possa estar errado. Deveria ser diagonal primária subtraindo diagonal secundária.