Olá amigos estudantes! Vamos aprender a calcular determinantes? Nesta página apresentaremos as ferramentas para o cálculo de determinantes das matrizes 2×2, 3×3, 4×4,…
Confira em nosso material didático as publicações sobre matrizes para um melhor entendimento sobre o conteúdo que segue.
Bom estudo!
DEFINIÇÃO
Determinante é um número ao qual está associada uma matriz quadrada, portanto só possui determinante uma matriz que possua o número de linhas igual ao número de colunas. Esse número é obtido quando se opera com os elementos dessa matriz.
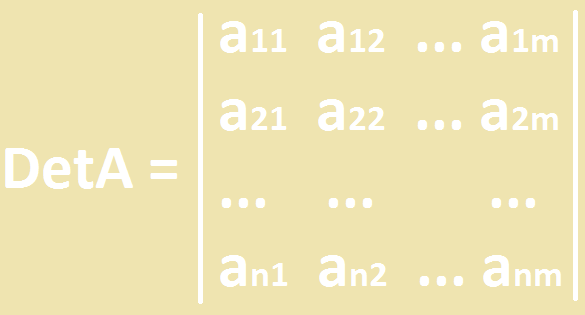
Dada uma matriz A, denotaremos determinante de A como “DetA”.
MATRIZES DE ORDEM 1
Seja a matriz A, de ordem n = 1, então o seu determinante será o único elemento da matriz A.
Exemplo:
A = (5)
DetA = 5
MATRIZES DE ORDEM 2 OU 3
Devido ao fato dessas matrizes serem as mais utilizadas em exercícios ou questões de concursos, apresentamos a forma de calculo com mais detalhes e exemplos. Basta clicar nos links abaixo:
Como calcular determinantes de matrizes 2×2
Como calcular determinantes de matrizes 3×3
MATRIZES DE ORDEM 4 OU SUPERIOR
Existe uma ferramenta muito importante que serve para calcularmos o determinante de matrizes 4×4, 5×5, …, é o chamado Teorema de Laplace. Clique no link abaixo para acompanhar com mais detalhes a definição e os exemplos de como utilizar este teorema:
PROPRIEDADES DOS DETERMINANTES
P1: Fila Nula
Se a matriz A possui uma fila na qual todos os elementos são iguais a zero, então det A = 0
P2: Troca de filas paralelas
Dada a matriz A, ao trocarmos quaisquer filas paralelas de A, obtemos uma nova matriz A’, onde det A = det A’, ou seja, o valor do determinante não é alterado.
P3: Multiplicação de uma fila por um número real qualquer
Dada a matriz B, ao multiplicar qualquer fila de B por um número real k, obtemos uma nova matriz B’, de modo que det B’ = k.det B, ou seja, o valor do determinante da nova matriz é o determinante anterior multiplicado pelo número real utilizado.
P4: Filas paralelas iguais ou proporcionais
Toda matriz que possui filas paralelas iguais ou proporcionais possui determinante = 0
ô Jordan que material bacana que voce postou para ajudar as pessoas a estudar,obrigada
Obrigado Maria.
Volte sempre!
Parabéns Professor!
Muito didático e objetivo seu material. Está me ajudando bastante.