Você sabe qual é a derivada da função composta? Veremos aqui um método interessante, chamado de regra da cadeia, e utilizado para o calculo da derivada deste tipo de função.
Não deixe de ver também nossos conteúdos sobre outros tópicos do cálculo diferencial.
Bom estudo!
Se g for derivável em x e f for derivável em g(x), então a função composta F = fog definida por F(x) = f(g(x)) é derivável em x e F ‘ é dada pela seguinte fórmula:
![]()
Também podemos utilizar a notação de Leibniz, se y=f(u) e u=g(x) forem deriváveis, então:
![]()
Exemplo 1. Utilizar a regra da cadeia para calcular a derivada da função F(x) = sen(x²).
Temos que a função de fora é a função seno, enquanto a função de dentro é uma função quadrática. Veja:
F'(x) = f'(g(x)).g'(x)
F'(x) = cos(x²).2x
F'(x) = 2x.cos(x²)
Pela notação de Leibniz teríamos:
y = f(u) = sen(u)
u = g(x) = x²

Exemplo 2. Calcular a derivada da função F(x) = (senx)².
Temos que a função de fora é uma função quadrática (y=x²), e a função de dentro é a função seno. Veja:
F'(x) = f'(g(x)).g'(x)
F'(x) = 2.(senx).(cosx)
F'(x) = 2.senx.cosx
Pela notação de Leibniz teríamos:
y = f(u) = u²
u = g(x) = senx
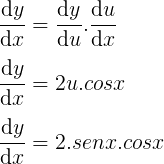
Gostou do nosso conteúdo sobre a derivada da função composta (regra da cadeia)?
Deixe o seu comentário.
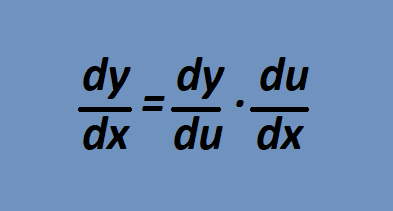
Gostei, conteúdo explicitado.