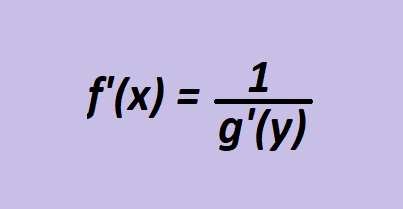Você sabe qual é a derivada de uma função inversa? Veremos aqui uma fórmula muito simples e muito útil em alguns tipos de funções.
Não deixe de ver também as nossas publicações sobre outros tópicos do cálculo diferencial.
Bom estudo!
Seja y = f(x) uma função bijetora (inversível) e derivável no intervalo ]a,b[, tal que f'(x)≠0 para todo x∈]a,b[.
A função inversa de y = f(x), representada por x=g(y), é derivável no ponto y, sendo y = f(x).
Como y = f(x) e x = g(y), temos:
x = g(f(x))
Utilizando a regra da cadeia, vamos descobrir qual é a derivada da função inversa derivando a igualdade acima em relação à variável x:
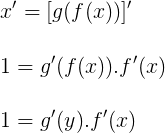
De onde concluímos que:
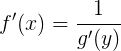
Exemplo. Calcular a derivada de y = √x, com x>0.
É fácil concluir que a função x = y² é a inversa de y = √x, observando que x>o.
Derivando a função inversa:
x’ = 2y
Utilizando a regra que acabamos de descobrir:
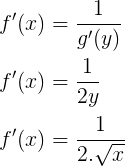
Aprendeu a calcular a derivada da função inversa? Tem mais alguma dúvida?
Deixe o seu comentário.