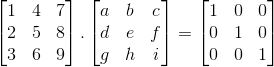Nesta página vamos aprender a identificar e como calcular a matriz inversa, muito útil no estudo da álgebra linear.
O processo é um pouco trabalhoso e envolve alguns conceitos e operações entre matrizes, por isso não deixe de ler previamente os outros conteúdos sobre o assunto.
Bom estudo!
DEFINIÇÃO
Seja A uma matriz quadrada de ordem n. A é dita invertível (ou inversível) se existir uma outra matriz B, onde:
A.B = B.A = In
Neste caso dizemos que B é a matriz inversa de A e é representado por A-1.
COMO SABER SE A MATRIZ É INVERTÍVEL
Uma matriz quadrada A é invertível se, e somente se, detA ≠ 0.
Vamos calcular o determinante das matrizes abaixo para sabermos se são invertíveis.
Exemplo 1:
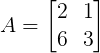
detA = 2.3 – 6.1 = 0
Logo, A não é inversível.
Exemplo 2:
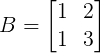
detB = 1.3 – 1.2 = 1
Logo, B é inversível.
CALCULANDO A MATRIZ INVERSA
Agora que já aprendemos a identificar se uma matriz possui ou não inversa, vamos aprender a calcular em 3 passos simples, onde utilizaremos a matriz B (exemplo 2), onde já sabemos que a inversa existe.
Conforme a definição apresentada, a matriz inversa B-1 deve atender a seguinte condição:
B.B-1 = B-1.B = In
Primeiro passo: Determinar a matriz B-1, tal que B.B-1 = In.
Como não sabemos nenhum dos elementos de B-1, vamos considerar cada um deles como incógnitas (x, y, z, w).
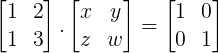
Aplicando os nossos conhecimentos sobre o produto de matrizes:
1) x + 2z = 1
2) y + 2w = 0
3) x + 3z = 0
4) y + 3w = 1
Chegamos em um sistema de 4 incógnitas e 4 equações. Vamos resolvê-lo:
Fazendo (equação 3) – (equação 1):
x + 3z – x – 2z = 0 – 1
z = -1
Como z = -1, pela equação 1:
x + 2z = 1
x + 2.(-1) = 1
x – 2 = 1
x = 3
Fazendo (equação 4) – (equação 2):
y + 3w – y – 2w = 1 – 0
w = 1
Como w = 1, pela equação 2:
y + 2w = 0
y + 2.1 = 0
y = -2
Agora que descobrimos os valores das incógnitas, nossa matriz B-1 será:
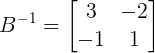
Segundo passo: Tirar a “prova real”, ou seja, conferir se vale o produto B.B-1 = In.
Deixaremos a cargo do estudante conferir que:
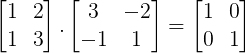
Terceiro passo: Conferir se vale o produto B-1.B= In.
Como já sabemos, a ordem do produto, no caso de matrizes, altera sim o resultado. Por isso devemos conferir a multiplicação alterando a ordem.
Também deixaremos a cargo do estudante conferir que:
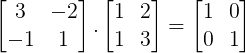
CALCULANDO A INVERSA DE MATRIZES 3×3, 4×4
Em nosso exemplo calculamos a inversa de uma matriz 2×2, que possui 4 elementos o que nos obrigou a utilizar 4 incógnitas.
Caso seja necessário calcular a inversa de uma matriz maior, devemos também utilizar uma quantidade maior de incógnitas, a saber:
Matriz 3×3: 9 incógnitas
Matriz 4×4: 16 incógnitas
Matriz 5×5: 25 incógnitas
…
Matriz nxn: n² incógnitas
Veja o exemplo no caso de uma matriz 3×3: