Dando continuidade ao estudo da trigonometria, nesta página apresentaremos a definição de ciclo trigonométrico.
Pede-se que o aluno já possua conhecimentos acerca do plano cartesiano, circunferência e ângulos.
Bom estudo a todos.
DEFINIÇÃO
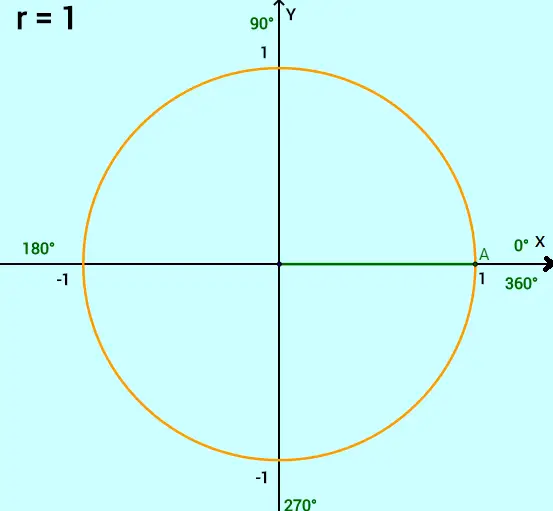
O ciclo trigonométrico nada mais é do que uma circunferência de raio unitário (igual a 1), cujo centro está localizado no ponto (0, 0) do plano cartesiano. Veja a figura:
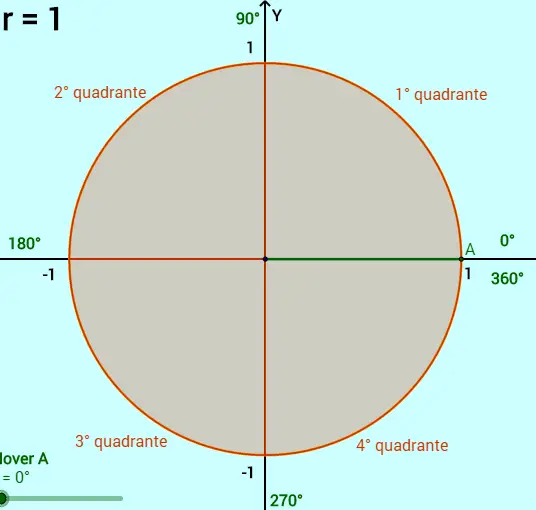
QUADRANTES
O ciclo trigonométrico é dividido em quatro partes, chamadas de quadrantes e identificados de acordo com o sentido anti horário, partindo-se do ângulo 0º. Veja a figura:
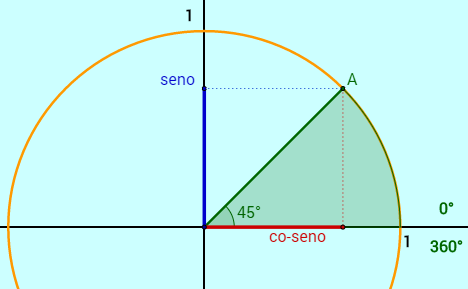
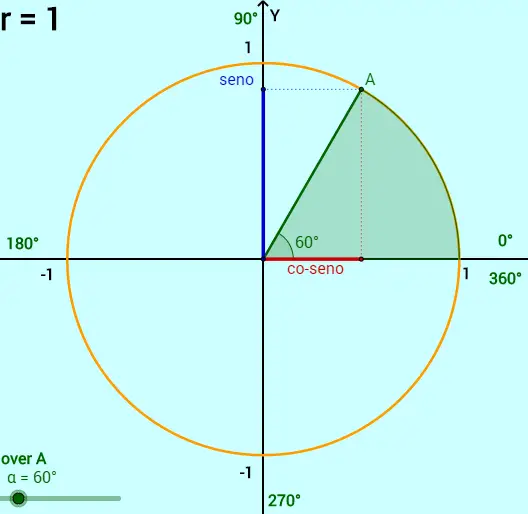
LOCALIZANDO O SENO E O COSSENO
O fato do ciclo trigonométrico possuir raio unitário facilita e muito os nossos cálculos. Veja na figura abaixo que quando tomamos o ângulo de 60º, o ponto A associado a ele pode ser localizado no plano cartesiano através das coordenadas (cos60º, sen60º). Isto pode ser verificado facilmente apenas sabendo que o raio que liga o centro e o ponto A também é hipotenusa do triângulo retângulo onde está localizado o ângulo de 60º.
Generalizando, dado um ponto da circunferência, suas coordenadas serão o cosseno e o seno do ângulo associado a este ponto. Assim, os sinais do seno e cosseno variam de acordo com o quadrante. Veja:
- O seno será positivo nos quadrantes I e II e negativo nos quadrantes III e IV.
- O cosseno será positivo nos quadrantes I e IV e negativo nos quadrantes II e III.
O SINAL DA TANGENTE
A tangente, como já sabemos, pode ser calculada através da divisão do seno pelo cosseno. Como já sabemos os sinais do seno e do cosseno nos quatro quadrantes, podemos calcular facilmente o sinal da tangente. Veja:
- No primeiro quadrante, o seno e o cosseno são positivos, logo a tangente também o será.
- No segundo quadrante, o seno é positivo e o cosseno é negativo, logo a tangente será negativa.
- No terceiro quadrante, o seno e o cosseno são negativos, logo a tangente será positiva.
- No quarto quadrante, o seno é negativo e o cosseno é positivo, logo a tangente será negativa.
REPRESENTAÇÃO GEOMÉTRICA DA TANGENTE
Agora que já sabemos que a coordenada x representa o cosseno e a coordenada y representa o seno, vamos aprender a representar geometricamente a tangente.
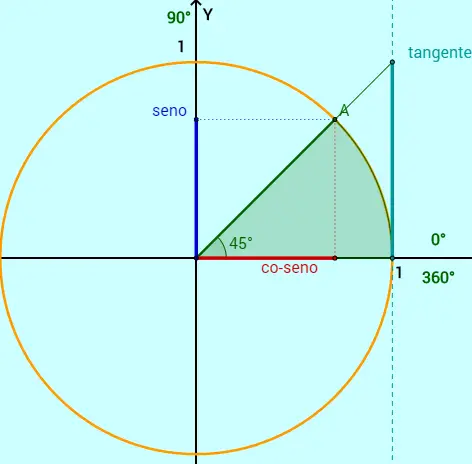
Veja na figura que a tangente de 45º está localizada na reta x=1, delimitada pelo ponto (1, 0) e o ponto de interseção da reta x=1 com a reta que passa por A e pelo centro.