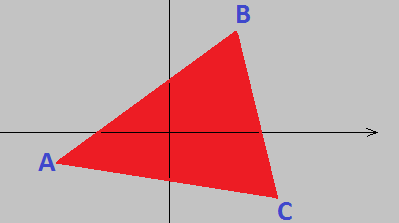
Estudando matemática para concursos? Confira aqui como é possível calcular a área de um triângulo pela geometria analítica.
Não deixe de ver também nossos conteúdos sobre os outros tópicos da geometria analítica.
Bom estudo!
A fórmula que calcula a área de um triângulo na geometria plana é uma das mais famosas que existem na matemática. Vamos relembrar?
![]()
Onde:
A = área
b = base
h = altura
Nesta página vamos aprender a calcular a área de um triângulo sem conhecer o valor dessas medidas. Vamos utilizar alguns conceitos de geometria analítica, onde será necessário saber apenas as coordenadas dos três vértices do triângulo.
Considere o triângulo ABC, cujas coordenadas dos vértices são A(xA, yA), B(xB, yB) e C(xC, yC), apresentado na figura abaixo:
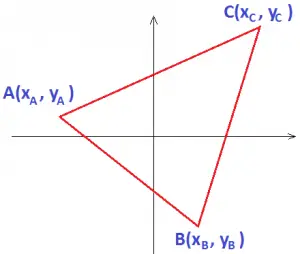
A fórmula que calcula a área de um triângulo através da geometria analítica é a seguinte:
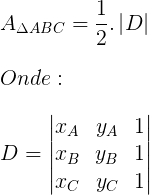
Exemplo. Calcular a área do triângulo de vértices A(1,2), B(3, 3) e C(0, 5).
Temos:
xA = 1
yA = 2
xB = 3
yB = 3
xC = 0
yC = 5
Calculando o determinante através da regra de Sarrus:
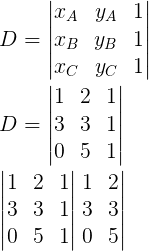
Det = 0.3.1 + 5.1.1 + 1.3.2 – 1.3.1 – 2.1.0 – 1.3.5
Det = 0 + 5 + 6 – 3 – 0 – 15
Det = -7
Calculando a área do triângulo:
A = (1/2) . |D|
A = (1/2) . |-7|
A = (1/2) . 7
A = 7/2
Gostou da nossa página sobre o cálculo da área de um triângulo na geometria analítica?
Curta e compartilhe nas redes sociais.